Задача 8452 Найдите все значения а, при каждом из...
Условие
Решение
(х+2)(х²-5х+10)=а+19;
х³ -3х²+1=a;
Рассмотрим
f(x)=х³ -3х²+1
f`(x)=3x²-6x
f`(x)=0
x=0 и x=2 точки возможного экстремума.
Проверяем выполнение достаточного условия экстремума, находим знак производной
[-1]__+__(0)__-_____(2)__+_[2,5]
На [-1;0) и на (2;2,5] функция возрастает, на
(0;2)- убывает.
х=0- точка максимума, х=2- точка минимума
f(0)=1
f(2)=8-12+1= - 3
f(-1)=-1-3+1= - 3
f(2,5)=(2,5)³-3•(2,5)²+1=-2,125
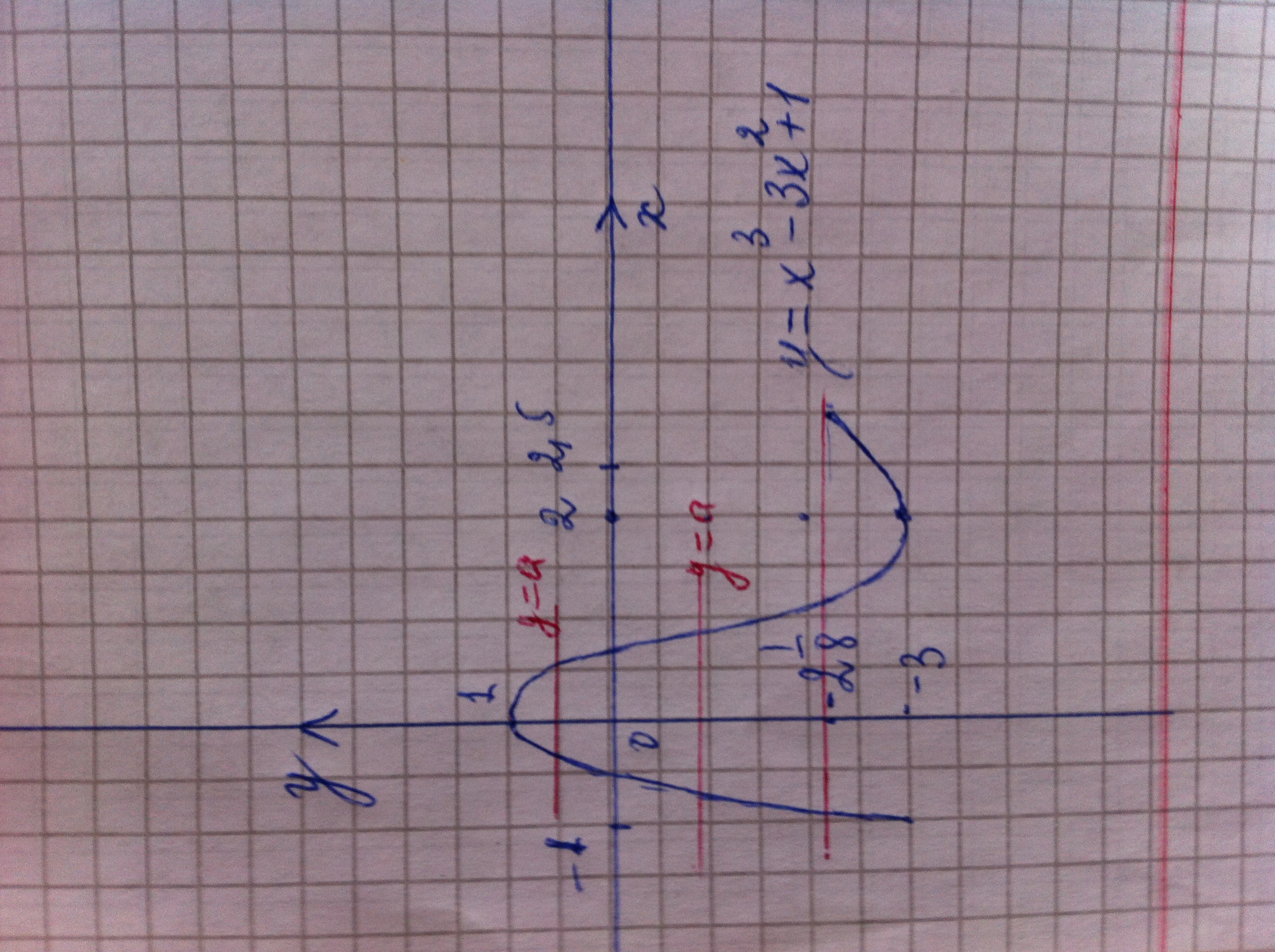
см. график на рисунке.
По рисунку видим, что прямые у=а будут пересекаться с графиком ровно в двух точках
при а∈{–3} U (–2,125 ;1)
О т в е т.а∈{–3} U (–2,125 ;1)
Все решения
