Задача 8449 Решите неравенство...
Условие
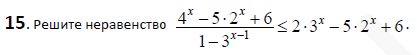
Решение
2^(x)=t; 4^(x)=t²; 3^(x)=u. 1-3^(x-1)=1-((3^(x))/3)=1-(u/3)
(t²-5t+6-(2u-5t+6)(1-(u/3)))/(1-(u/3))<=0
(t²-5t+6-2u+5t-6+(2u²/3)-((5ut)/3)+2u)/(1-(u/3)<=0
(t²+(2u²/3)-((5ut)/3))/(1-(u/3)<=0
Числитель разложим на множители как квадратный трехчлен относительно переменной t
at²+bt+c=a(t-t₁)(t-t₂)
t²-((5u)/3)t+(2u²/3)=0
D=(25u²/9)-4*((2u²/3)=(25u²/9)-4*((6u²/9)=u²/9
t₁= (((5u)/3)-(u/3))/2=2u/3 t₂=(((5u)/3)+(u/3))/2=u
t²-((5u)/3)t+(2u²/3)=(t-(2u/3))(t-u)
Решаем неравенство
(2^(x)-2*3^(x-1))(2^(x)-3^(x))/(1- 3^(x-1)) <=0
Неравенство сводится к четырем системам.
1) 1 - 3^(x-1)>0
2^(x)-2*3^(x-1)<=0
2^(x)-3^(x)>=0
х<1
x>=1
x ≤ 0
система не имеет решений.
2)1 - 3^(x-1)>0
2^(x)-2*3^(x-1)>=0
2^(x)-3^(x)<=0
x<1
x<=1
x ≥ 0
решение системы
[b]0 ≤ x<1[/b]
3)1 - 3^(x-1)<0
2^(x)-2*3^(x-1)>=0
2^(x)-3^(x) ≥ 0
x>1
x<=1
x ≤ 0
система не имеет решений
4)1 - 3^(x-1)>0
2^(x)-2*3^(x-1) ≤ 0
2^(x)-3^(x) ≥ 0
х>1
x>=1
x ≤ 0
нет решений
[blue]О т в е т. [0;1)[/blue]
Все решения
