Задача 8443 Постройте график функции y=|(x-2)/x| и...

larisashakirova

09.04.2016

Постройте график функции y=|(x-2)/x| и определите при каких значениях а прямая у=ах имеет с графиком ровно две общие точки.

Преобразуем функцию: у=|1-2/x|, x≠0. По определению модуля |x|=x, если x≥0, |x|=-х, если х<0 => y=1-2/x, если x≥2, y=-1+1/x, если x<2. Построим графики на данных промежутках. При x≥2 гипербола, ветви расположены во второй и четвертой четвертях, сдвиг графика на 1 вверх. При x<2 гипербола, ветви расположены в первой и третьей четвертях, сдвиг графика на 1 вниз.
Прямая у=а будет иметь с графиком ровно две общие точки при а>0. Вычислим значение а.
|1-2/x|=ax => при x<2 1-2/x=ax => (x-2-ax^2)/x=0 => x-2-ax^2=0, x≠0. Квадратное уравнение имеет два корня, если дискриминант больше 0.
D=1-4•(-2)•(-a)=1-8a>0 => a<1/8.
При x≥2 -1+2/x=ax => -1+2/x-ax=0 => (-x+2-ax^2)/x=0 => -x+2-ax^2=0, x≠0.
D=1-4•2•(-a)=1+8a>0 => a>-1/8, a>0 => 0<a<1/8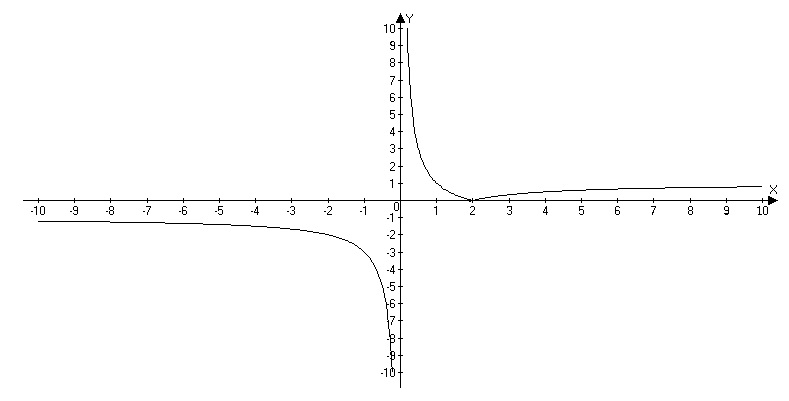

Ответ: 0<a<1/8

u851401142

25.03.2017

Найдите значение р при котором числа р-3,корень из 4р, р+2 являются тремя членами геометрической прогрессии.