Задача 8406 Найдите значения параметра b, при...
Условие
(|x|+5)^2+(y-4)^2=4,
(x+2)^2+y^2=b^2
Решение
получаем
(x+5)²+(y–4)²=4 - окружность с центром (-5;4) радиусом 2.
Но эта окружность не принадлежит правой полуплоскости
аналогично
при х<0
получаем
(-x+5)²+(y–4)²=4 - окружность с центром (5;4) радиусом 2.
Но эта окружность не принадлежит левой полуплоскости
Поэтому первое уравнение не имеет решений вообще.
Если бы было
(|x|-5)²+(y–4)²=4
то окружности располагались бы в соответствующих полуплоскостях, тогда можно о чем-то говорить.
при х>=0
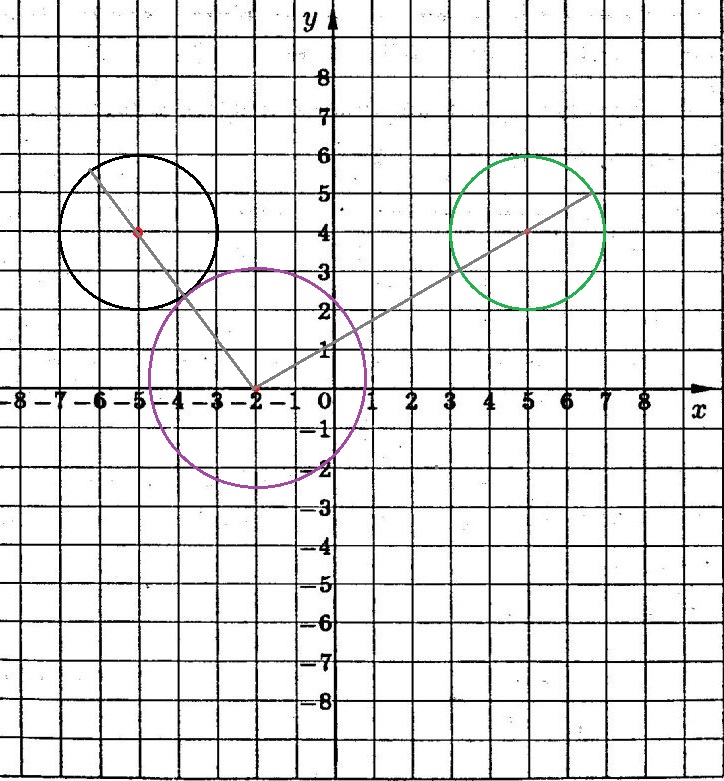
(x-5)²+(y–4)²=4 - окружность с центром (5;4) радиуса 2 ( зеленого цвета)
при х <0
(-x-5)²+(y–4)²=4 - окружность с центром (-5;4) радиуса 2 (черного цвета)
Второе уравнение задает окружность с центром в точке (-2;0) радиусом b (сиреневого цвета)
Надо найти случаи, когда сиреневая окружность будет касаться одной из окружностей
cм. рисунок