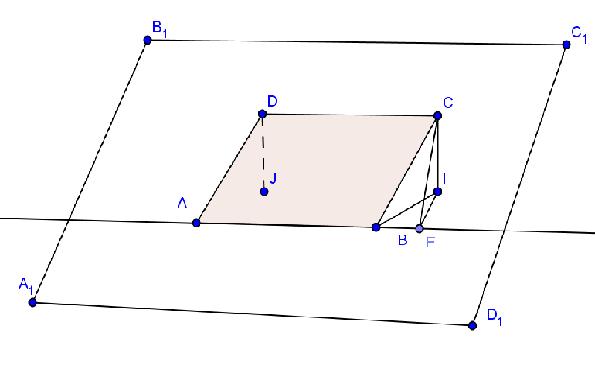
Задача 839 Сторона АВ ромба ABCD равна a, один из...

Гость

29.03.2014

Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость альфа на расстоянии а/2 от точки D.
а) Найдите расстояние от точки С до плоскости альфа.
б) Покажите на рисунке линейный угол двугранного угла DABM, М принадлежит плоскости альфа.
в) Найдите синус угла между плоскостью ромба и плоскостью альфа.

slava191

10.09.2015

★

AB||CD||IJ, DJ||CI, т.к. это перпендикуляры к одной плоскости, значит CDJI – параллелограмм, значит DJ=CI = альфа/2.

Выберем такую точку Е на прямой АВ, что IE и CE перпендикулярны АВ. Тогда угол CEI – искомый угол между плоскостями ромба и альфа. Из прямоугольного CIB получим:
BI = sqrt(CB^2-CI^2) = sqrt(3/4альфа)
Из прямоугольного CEB: CE = CB*sin(60граусов) = альфа*sqrt(3)/2. Значит из прямоугольного CIE получим sin CEI = CI/CE = альфа*2/(2*альфа*sqrt(3)) = 1/sqrt(3)