Задача 8379 Решите неравенство log(x^2-6x+9)(7-x)...
Условие
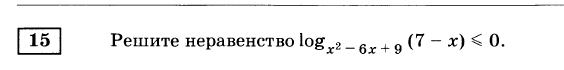
математика 10-11 класс
14107
Решение
★
Применяем метод рационализации логарифмических неравенств:
{(x^2-6x+9-1)*(7-x-1) меньше или равно 0;
{x^2-6x+9 > 0
{x^2-6x+9 ≠1
{7-x > 0
{(x-2)(x-4)(x-6) больше или равно 0
{x≠3
{x≠2 и х≠4
{x < 7
О т в е т. (2;3)U(3;4)U[6;7)