Задача 8347 ...

Julia_Trusova

04.04.2016

В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N - середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием - сечение пирамиды SABC плоскостью α.

Плоскость (MNK)-плоскость α
SA=SB=SC=8, AB=AC=BC=12
SO-высота пирамиды
СЕ - и медиана, и высота, => СЕ=sqrt(ВС^2-EB^2)=sqrt(144-36)=6sqrt(3)
O-центр треугольника АВС, О-точка пересечения медиан, так как треугольник АВС-правильный.
СО=2/3*СЕ=2/3*6sqrt(3)= 4sqrt(3), а ЕО=1/3*СЕ=1/3*6sqrt(3)= 2sqrt(3)

а)MN-средняя линия треугольника ASB, => MN||AB и EP=PS
PH⊥(ABC); => PH||SO; PH-средняя линия ΔSEO
=>H-середина ЕО, т.е. ЕН=НО=(2sqrt(3))/2=sqrt(3)
НС=ОС+ОН=4sqrt(3)+ sqrt(3)= 5sqrt(3)
СН/ЕН=(5sqrt(3))/sqrt(3)=5/1

б)СMNKD- пирамида, вершиной которой является точка C, а основанием - сечение пирамиды SABC плоскостью α.
СН⊥(АМN)
=>CH-высота
MNKD-основание пирамиды, равнобедренная трапеция
РН=1/2*SO
SO=sqrt(SC^2-CO^2)=sqrt(64-48)=4
ΔDCK~ΔACB(по двум углам)
=>k=CH/CE=5/6
=>DK/AB=5/6
DK/12=5/6
DK=(12*5)/6=10
MN=1/2*AB=6
V(СMNKD)=1/3*S(MNKD)*h=1/3*(6+10)/2*2*5sqrt(3)=(80sqrt(3))/3


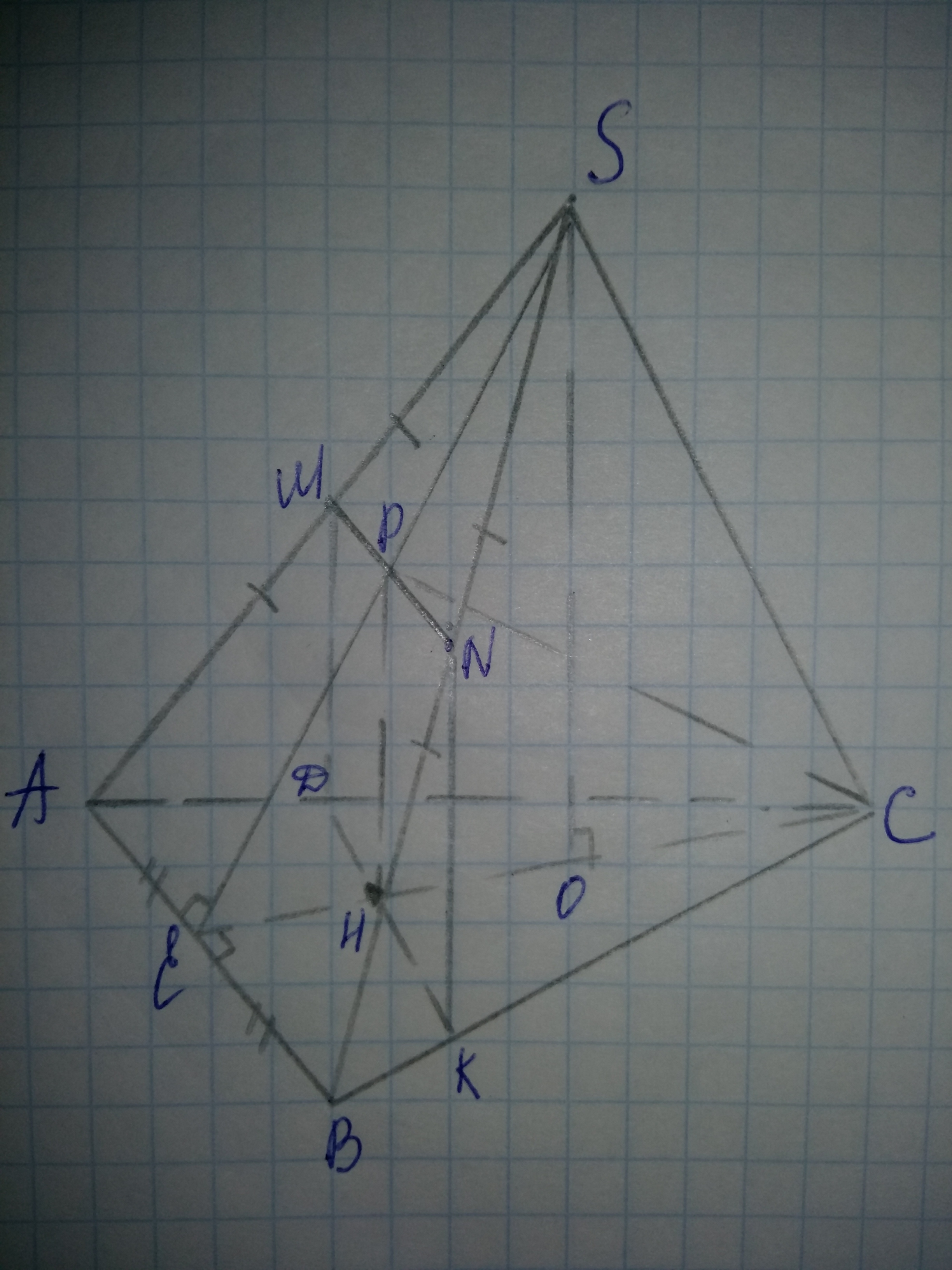
Ответ: 80sqrt(3)/3