Задача 8338 Дан выпуклый четырехугольник ABCD со...

Julia_Trusova

03.04.2016

Дан выпуклый четырехугольник ABCD со сторонами AB=3, BC=CD=5, AD=8 и диагональю АС=7.

а)Докажите, что около него можно описать окружность.
б)Найдите диагональ BD.

а)Около четырехугольника можно описать окружность, если суммы углов равны 180°.
По теореме косинусов из треугольника АВС:
АC^2=AB^2+CB^2-2*AB*CB*cos∠B
49=9+25-30*cos∠B
cos∠B=15/(-30)=-1/2
По теореме косинусов из треугольника АDС:
АC^2=AD^2+CD^2-2*AD*CD*cos∠D
49=64+25-80*cos∠D
cos∠D=(-40)/(-80)=1/2
Таким образом косинусы углов B и D противоположны, значит ∠В+∠D=180° и около четырехугольника можно описать окружность.

б)По теореме косинусов из треугольника BAD:
BD^2=BA^2+DA^2-2*BA*DA*cos∠A
BD^2=9+64-48*cos∠A
cos∠A=(73-BD^2)/48
По теореме косинусов из треугольника ВСD:
BD^2=BC^2+DC^2-2*BC*DC*cos∠C
BD^2=25+25-50*cos∠C
cos∠C=(50-BD^2)/50
Угла А и С так же в сумме дают 180 градусов, значит значения косинусов этих углова противоположны, таким образом:
(73-BD^2)/48=-(50-BD^2)/50
(73-BD^2)/48=(BD^2-50)/50
(73-BD^2)*50=(BD^2-50)*48
73*50-50 BD^2=48 BD^2-48*50
48 BD^2+50 BD^2=73*50+48*50
98 BD^2=121*50
BD^2=(121*50)/98
BD^2=(121*25)/49
BD=(11*5)/7=55/7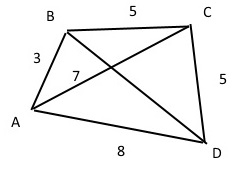

Ответ: 55/7