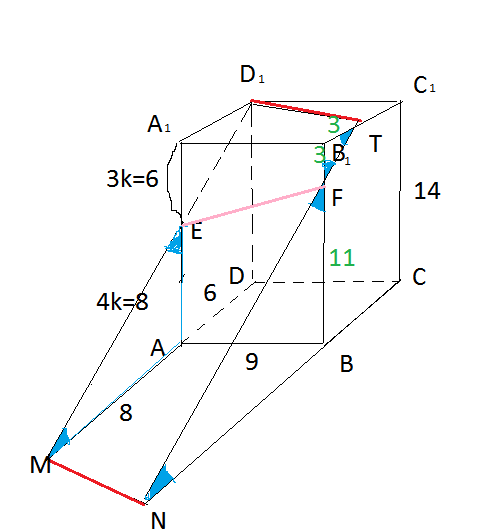
Задача 8315 На ребре AA1 прямоугольного...

vicktoriya2110

03.04.2016

На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка E так, что A1E:EA=3:4. Точка T - середина ребра B1C1. Известно, что AB=9, AD=6, AA1=14.

А) В каком отношении плоскость ETD1 делит ребро BB1?
В) Найдите угол между плоскостью ETD1 и плоскостью AA1B1.

SOVA

03.04.2016

★

Чтобы построить сечение, соединяем точку D1 и Е и продолжаем до пересечения с плоскостью основания АВСD.Для этого продолжаем DA до пересечения с D1E, получаем точку М.
Проводим DT, так как плоскости верхнего и нижнего оснований параллельны, то секущая плоскость пересекает их по параллельным прямым проводим MN || D1T.ВС пересекается с МN в точке N. Проводим TN, точка пересечения с В1В - точка F

Сечение D1EFT построено.

Треугольники МАЕ и МDD1 подобны. Из подобия
МА: MD= AE: DD1
МА=8
Треугольник МАЕ прямоугольный равнобедренный. Острые углы 45 градусов. Отмечены на рисунке синим цветом.
Из треугольника B1TF c такими же углами, находим B1F=3; FB=14-3=11
Ответ. а) BF:FB1=11:3

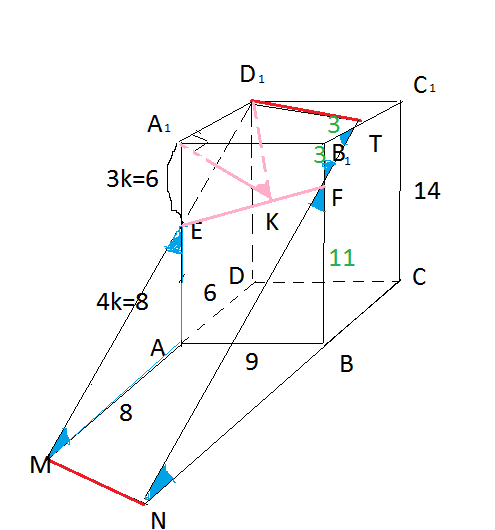
б) Плоскости пересекаются по прямой EF.
Проводим A1K⊥ EF.
Треугольник A1FD1- прямоугольный, так как A1D1 ⊥ плоскости A1B1BA, и потому A1D1 ⊥ EF.
По теореме о 3-х перпендикулярах D1K⊥ EF.

Из прямоугольной трапеции A1B1FE находим FE.
FE=sqrt((A1B1)^2+(A1E-BF)^2)=√90
Применяем метод площадей
Площадь треугольника A1EF, с одной стороны равна половине произведения основания А1Е на высоту А1В1, с другой -половине произведения основания EF на высоту А1К.
Поэтому
А1К*EF=A1E*A1B1
A1K=6*9/sqrt(90)=18sqrt(10)/10=9sqrt(10)/5

Из прямоугольного треугольника A1D1K:
tg ∠A1KD1=A1D1:A1K=6/(9√(10)/5)=30/(9sqrt(10))=10/(3*sqrt(10))=(sqrt(10))/3
∠A1KD1=arctg(√10/3)