Задача 8286 В треугольнике АВС проведена биссектриса...

Alex007

01.04.2016

В треугольнике АВС проведена биссектриса АМ. Прямая проходящая через вершину В перпендикулярно АМ , пересекает сторону АС в точке N; AB=6, BC=5, AC=9. Докажите что биссектриса угла С делит отрезок MN пополам. Пусть P- точка пересечения биссектрис треугольника АВС. Найдите отношение АР:PN

SOVA

01.04.2016

★

Биссектриса угла треугольника делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
ВМ:МС=АВ:АС=6:9=2:3
ВС=5
Значит, ВМ=2 и МС=3
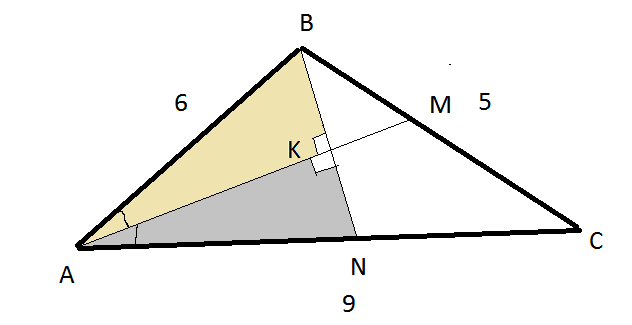
Биссектриса АМ и перпендикуляр из вершины B- пересекаются в точке К ( см. рис.1)
Δ АВК=ΔAКN по общему катету АК и острому углу
∠ВАК=∠КАN(АМ- биссектриса)
АВ=АN=6
NC=AC=AN=9-6=3
Треугольник МNC- равнобедренный, NC=MC=6
Биссектриса угла С равнобедренного треугольника одновременно является и медианой, поэтому делит MN пополам.

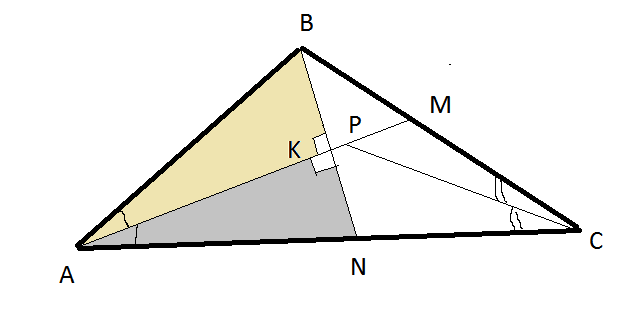
В треугольнике АМС биссектриса СР делит сторону АМ пропорционально прилежащим сторонам
АР:РМ=АС:СМ=9:3=3:1