Задача 8285 Решить неравенство...
Условие
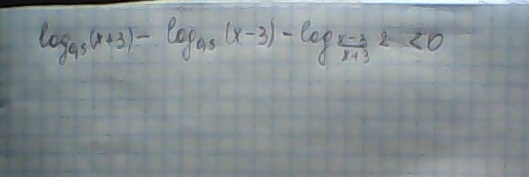
Решение

Все решения
Система
x+3>0
x-3>0
((x-3)/(x+3))>0
((x-3)/(x+3))≠ 1
ОДЗ:х>3
Применяем формулу перехода к другому основанию.
-log(2)(х+3)+log(2)(х-3)-1/(log(2)(x-3/x+3))<0
Заменим разность логарифмов логарифмом частного:
log(2)(x-3/x+3)-1/(log(2)(x-3/x+3))<0
Замена переменной
log(2)(x-3/x+3)=t
t-(1/t) <0
(t²-1)/t <0
-----(-1)----(0)-----(1)------
знаки : - + - +
t<-1 или 0< t < 1
Обратная замена
1) log(2)(x-3)/(x+3) < -1
или
2) 0 < log(2)(x-3)/(x+3)<1
1)log(2)(x-3)/(x+3) < log (2)(1/2) ;
Логарифмическая функция с основанием 2>1 - возрастающая, большему значению функции соответствует большее значение аргумента
(x-3)/(x+3)<1/2
(2х-6-(х+3))/2(х+3)<0
(x-9)/2(x+3) <0
-3 < x < 9
C учетом ОДЗ:
3 < x < 9
2) log(2)1 < log(2)(x-3)/(x+3)< log(2)2
1 < (x-3)/(x+3) < 2
Система
(х-3)/(х+3)>1
(x-3)/(x+3)<2
или
(-6)/(х+3) >0 ⇒ x+3 <0 ⇒ x < -3, не входит в ОДЗ
(-x-9)/(x+3)<0
Система не имеет решений
О т в е т. (3;9)
