Задача 8229 ...

Julia_Trusova

28.03.2016

В треугольнике ABC‍ проведены биссектрисы AA‍1‍ и CC‍1,‍ K и М —‍ основания перпендикуляров, опущенных из точки B‍ на прямые AA‍1‍ и CC‍1.‍

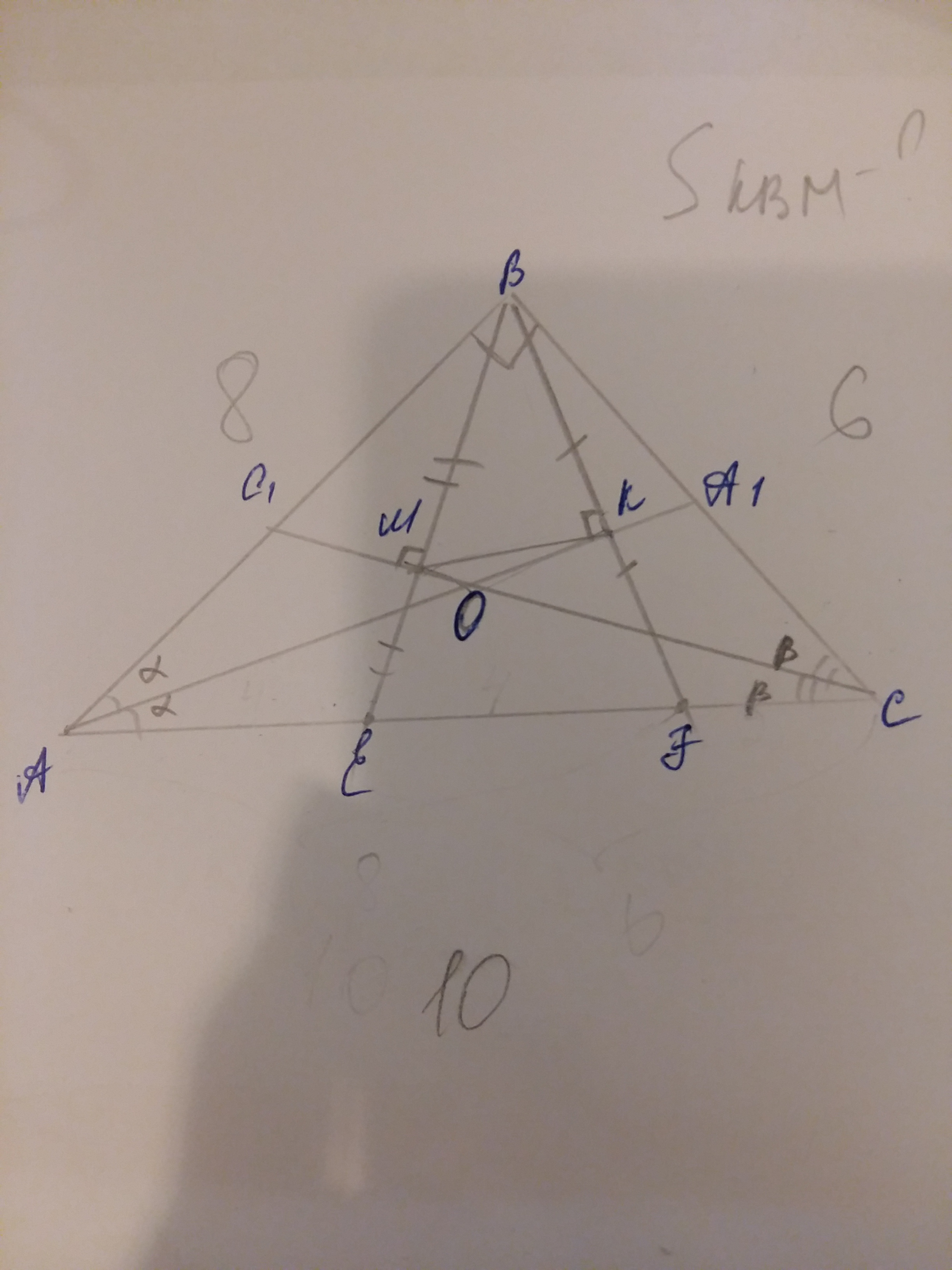
а) Докажите, что MK||AC.‍

б) Найдите площадь треугольника KBM, если известно, что AC=10, BC=6, AB=8.

а) Продолжим отрезки BM‍ и BK‍ до пересечения с прямой AC‍ в точках E‍ и F‍ соответственно.Высота AK треугольника ABF является его биссектрисой, значит, этот треугольник — равнобедренный, поэтому AK —‍ его медиана, т. е. K —‍ середина отрезка BF.‍
Аналогично М-середина отрезка ВЕ.
Отрезок MK —‍ средняя линия треугольника EBF,‍ поэтому MK||EF.‍ Следовательно, MK||AC.‍
б)Пусть ∠BAA1=∠A1AC=α,
∠BCC1=∠C1CA=β
Из △АВС по теореме обратной теореме Пифагора:
8^2+6^2=10^2
100=100
⇒ △АВС-прямоугольный, ∠АВС=90°.
⇒ ∠BAC+∠BCA=90°, тогда α+β=45°.
∠MOK=∠AOC=180°-45°=135°
Из MBKO: ∠MBK=360°-180°-135°=45°.
Из △АВС : cos(2α)=8/10=0,8,
тогда sinα=sqrt((1-cos(2α))/2)=sqrt((1-0,8)/2)=1/sqrt(10).
Из △ABK: BK=AB*sinα=8*1/sqrt(10)=8/sqrt(10).
Из △АВС : cos(2β)=6/10=0,6,
тогда sinβ=sqrt((1-cos(2β))/2)=sqrt((1-0,6)/2)=sqrt(2)/sqrt(10).
Из △BMC: BM=BC*sinβ=6*sqrt(2)/sqrt(10).
S(MBK)=1/2*BM*BK*sin45°=1/2*6*sqrt(2)/sqrt(10)*8/sqrt(10)*sqrt(2)/2=2,4



Ответ: 2,4