Радиус окружности, описанной около прямоугольного треугольника АВС с прямым углом С, равен 2,5. Радиус окружности, расположенной внутри угла АСВ, касающейся гипотенузы и продолжения катетов, равен 6. Найдите стороны треугольника АВС.
математика 8-9 класс
4919
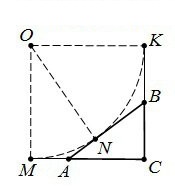
Радиус окружности описанной около прямоугольного треугольника равен половине гипотенузы => AB=5. OK и ОМ радиусы окружности, расположенной внутри угла АСВ, касающейся гипотенузы и продолжения катетов => OK⊥KC, OM⊥MC, KC⊥MC => ОКМС квадрат. Пусть NB=x, AN=5-x. KB=BN по теореме об отрезках касательных, проведенных из одной точке. KB=x, AM=AN=5-x. BC=KC-KB=6-x, AC=MC-MA=6-(5-x)=1+x. По теореме Пифагора BC^2+AC^2=AB^2 => (6-x)^2+(x+1)^2=25 => 36-12x+x^2+x^2+2x+1=25 => 2x^2-10x+12=0 => x^2-5x+6=0
D=25-24=1
x1=(5-1)/2=2
x2=(5+1)/2=3
Если КВ=2, то ВС=6-2=4, АС=2+1=3
Если КВ=3, то ВС=6-3=3, АС=3+1=4.
Т.е. катеты треугольника равны 3 и 4, гипотенуза 5.
Ответ: 3,4,5
