Задача 8222 ...

Julia_Trusova

28.03.2016

Окружность с центром O‍ касается боковой стороны AB‍ равнобедренного треугольника ABC,‍ продолжения боковой стороны AC‍ и продолжения основания BC‍ в точке N.‍ Точка M —‍ середина основания BC.‍

а) Докажите, что AN = OM.‍

б) Найдите OM,‍ если стороны треугольника ABC‍ равны 10, 10 и 12.

а) Пусть L —‍ точка касания данной окружности с прямой AC‍ (рис. 1). Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому AO —‍ биссектриса угла BAL.‍ Медиана AM‍ равнобедренного треугольника ABC‍ является его высотой и биссектрисой. Значит, ∠OAM = 90‍∘‍ как угол между биссектрисами смежных углов. Кроме того, ∠AMN = 90‍∘‍ и ∠MNO = 90‍∘‍ (радиус окружности, проведённый в точку касания, перпендикулярен касательной), поэтому AMNO —‍ прямоугольник. Диагонали прямоугольника равны, следовательно, AN = OM.‍

б) По теореме Пифагора из треугольника AMB‍ находим, что AM = sqrt(100-36)=sqrt(64)=8‍ (рис. 2). Пусть D —‍ точка касания данной окружности с боковой стороной AB‍ треугольника ABC.‍ Тогда BD = BN‍ и AD = AL,‍ значит,
CN + CL = (CB + BN) + (CA + AL) = (CB + BD) + (CA + AD) = CB + CA + (BD + AD) = CB + CA + AB = 10 + 12 + 10 = 32,‍
а так как CN = CL,‍ то CN = 1/‍2*32 = 16.‍
Тогда MN = CN − CM = 16 − 6 = 10.‍
Из прямоугольного треугольника AMN‍ находим что
AN = ‍sqrt(AM‍^2 + MN‍^2) = ‍sqrt(64 + 100) = 2‍sqrt(41).‍
Следовательно, OM = AN = 2‍sqrt(41).‍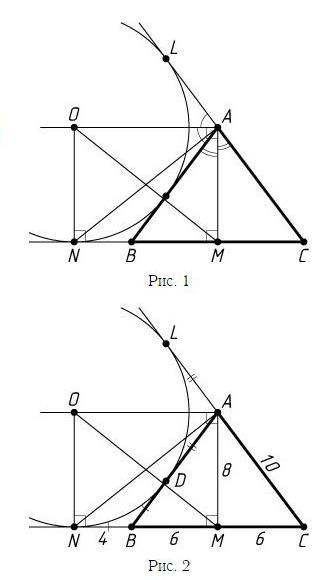

Ответ: 2sqrt(41)