Задача 8195 Дан треугольник ABC со сторонами AB=4,...

Julia_Trusova

28.03.2016

Дан треугольник ABC со сторонами AB=4, BC=6 и АС=8.

а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне ВС.

б) Найдите длину биссектрисы треугольника АВС, проведенной из вершины А.

а) О-центр вписанной окружности, АА1, ВВ1, СС1- медианы, М-точка пересечения медиан.
Расстояние от О до ВС: OK=r
r=S/p
S=sqrt(P*(p-a)*(p-b)*(p-c))
p=(4+6+8)/2=9
S(ABC)=sqrt(9*(9-4)*(9-6)*(9-8))=6sqrt(5)
r=6sqrt(5)/9=2sqrt(5)/3
Расстояние от М до ВС: МН(МН⊥ВС)
Так как медианы треугольника делят его на равновеликие треугольники, то S(BMC)=S(ABC)/3=6sqrt(5)/3=2sqrt(5)
S(BMC)=1/2*MH*BC
MH=S(BMC):1/2*BC
MH=2sqrt(5)/3
⇒ r=MH
⇒ MO||BC

б)Пусть АD-биссектриса,
тогда, AD=(2*sqrt(AB*AC*p*(p-BC)))/(AB+AC)
AD=(2*sqrt(4*8*9*(9-6)))/(4+8)=2sqrt(6)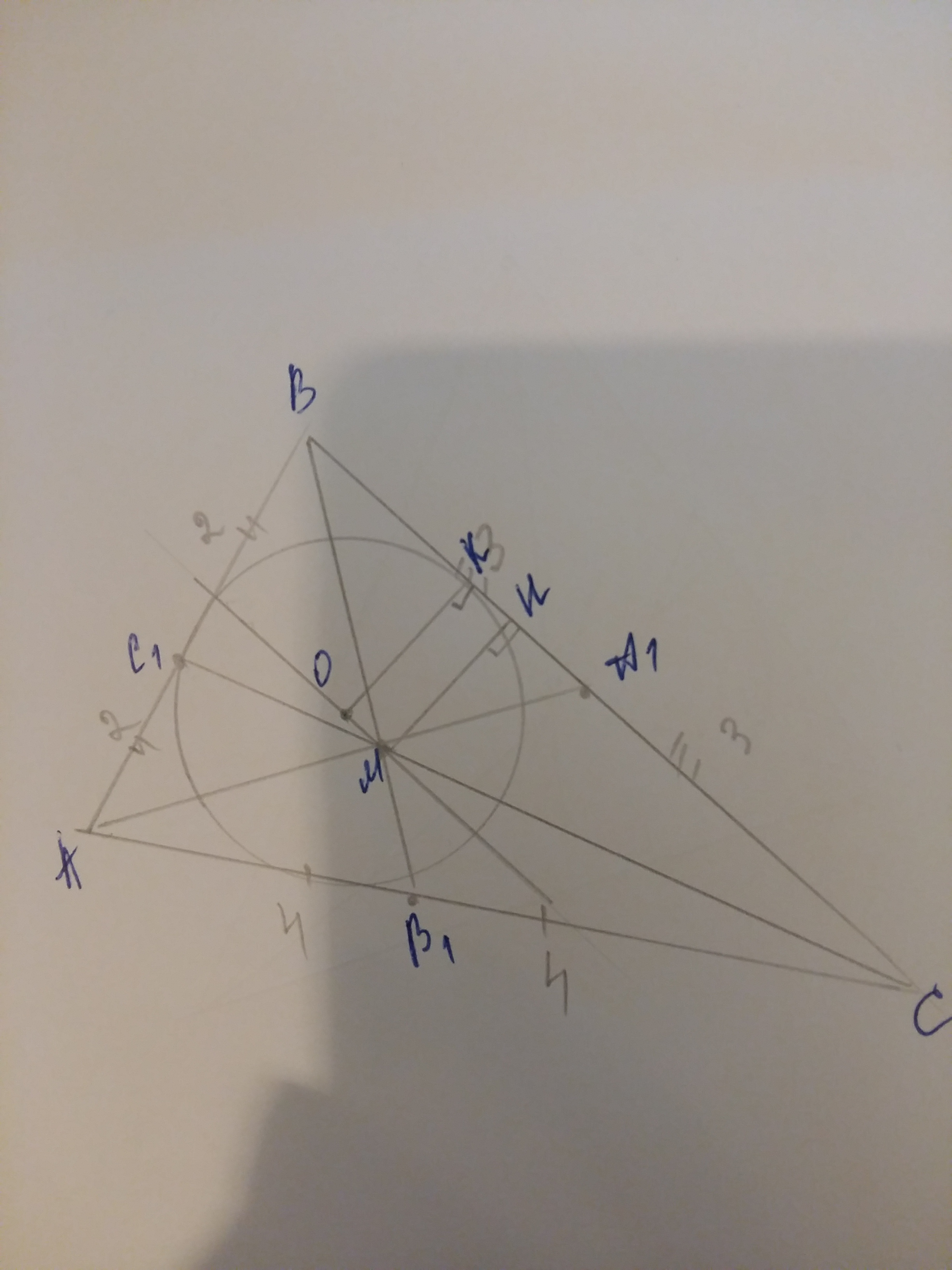

Ответ: 2sqrt(6)