Задача 8190 В равнобедренную трапецию ABCD с...

Julia_Trusova

27.03.2016

В равнобедренную трапецию ABCD с основаниями AD и BC вписана окружность, CH - высота трапеции.

а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке BH.

б) Найдите диагональ AC, если известно, что средняя линия трапеции равна 2sqrt(7), а угол AOD=120 градусов, где O - центр окружности, вписанной в трапецию, а AD - большее основание.

а)См. рис. 1
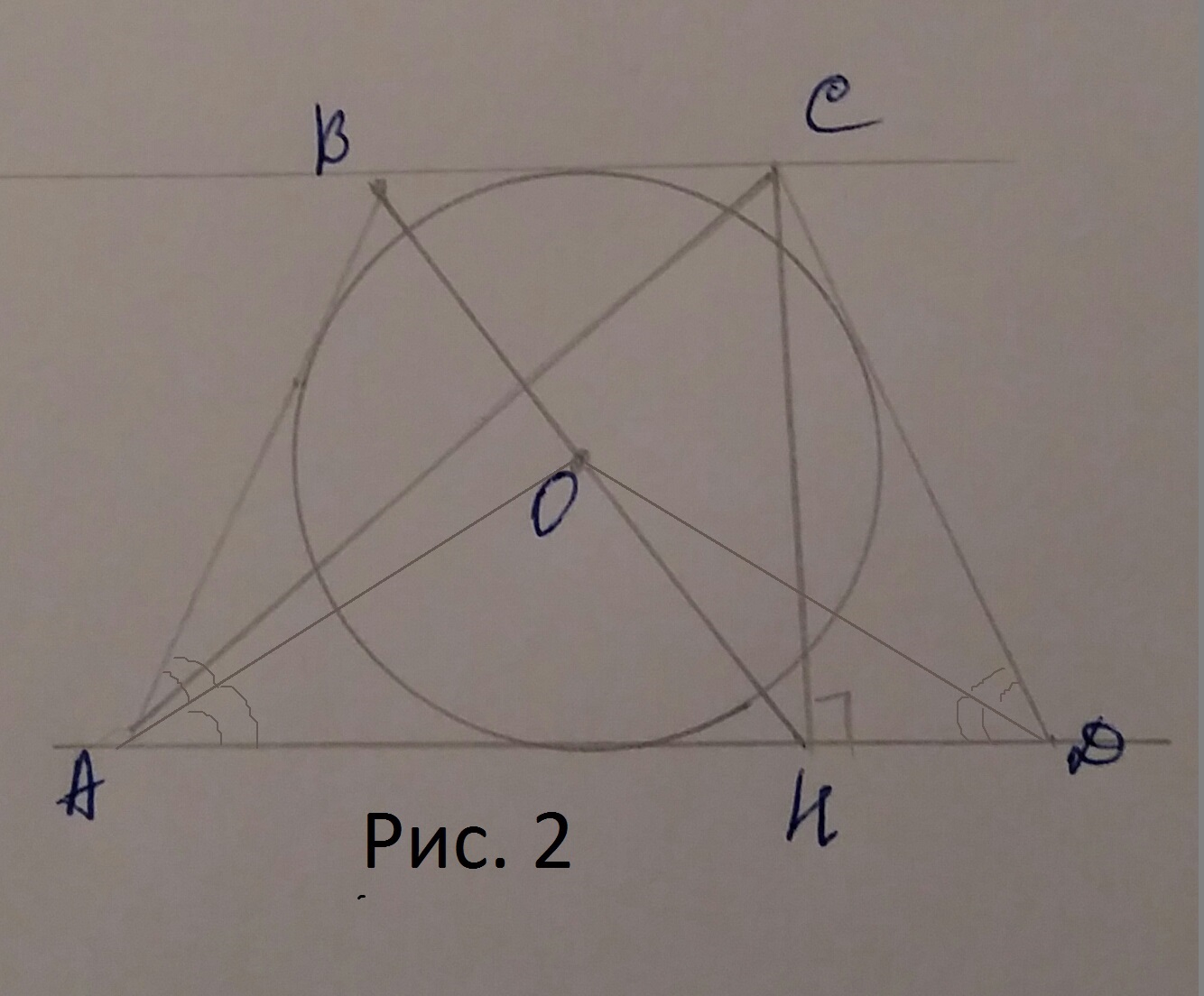
BG⊥AD; GBCH-прямоугольник
Пусть О=BH⋂CG
Докажем, что О-центр вписанной окружности.
KT⊥BC; OK=OT, т.е. О равноудалена от ВС и AD.
MN-средняя линия трапеции,
MN=CD по свойству описанной равнобедренной трапеции.
Тогда, ON=CN
⇒ △ONC-равнобедренный,
OF и CL его высоты, проведенные к равным сторонам,
⇒ OF=CL=KO, т.е. О равноудалена от BC,CD, AD(аналогично и от AB).
Значит, О-центр вписанной окружности и О∈ВН.

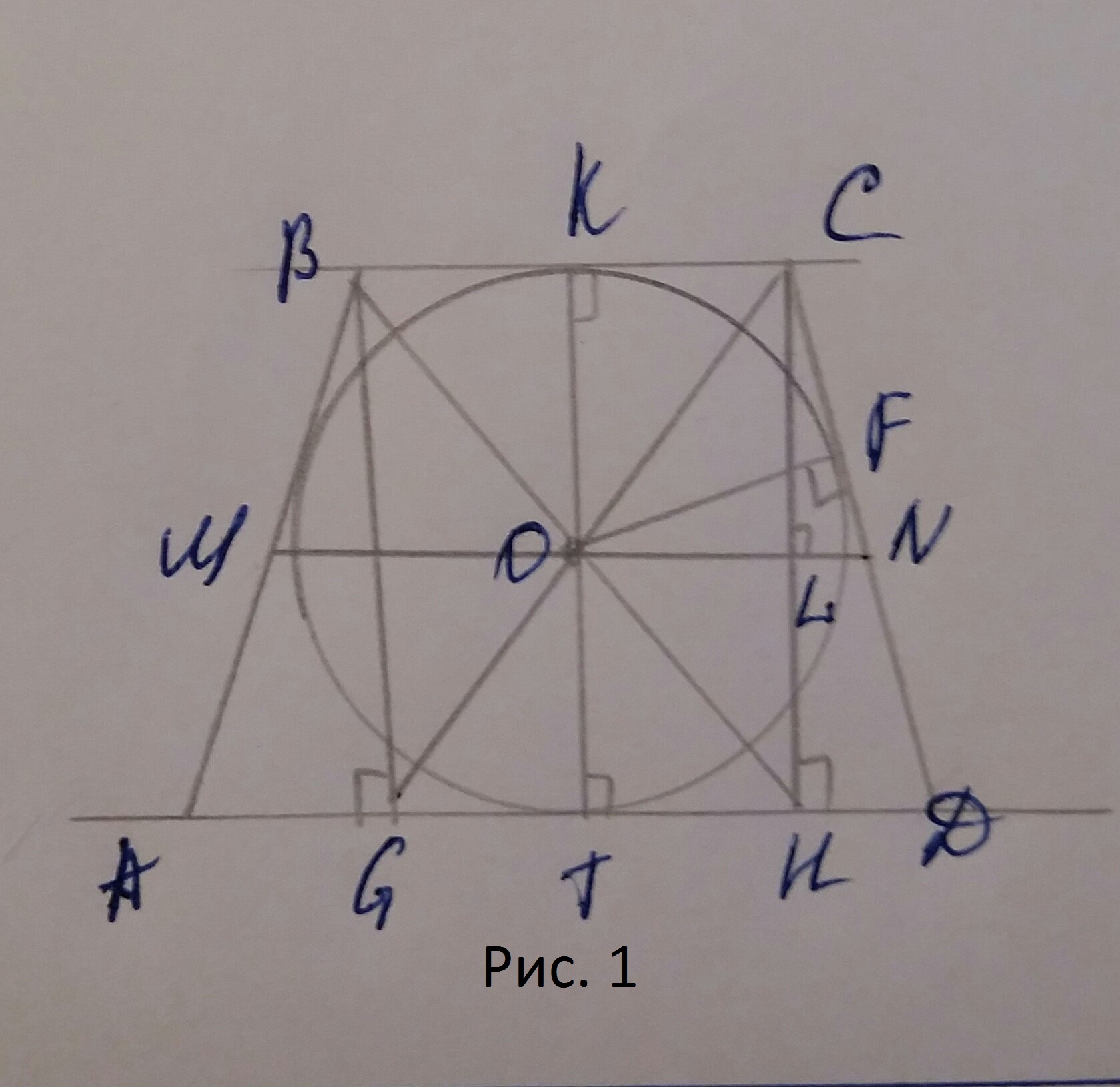
б)См. рис. 2
По свойству описанной равнобедренной трапеции CD=MN=2sqrt(7)
Из △AOD: ∠ADO=(180°-120°):2=30°.
∠ODC=∠ADO=30°(OD-биссектриса).
Из △CHD: ∠DCH=90°-60°=30°, ⇒HD=1/2*CD=1/2*2sqrt(7)=sqrt(7), по теореме Пифагора: CH=sqrt((2sqrt(7))^2-(sqrt(7))^2)=sqrt(28-7)=sqrt(21).
Так как трапеция описано около окружности AD+ВС=AB+CD=2sqrt(7)+2sqrt(7)=4sqrt(7)
AD=2HD+BC
Тогда, 2HD+BC+BC=4sqrt(7)
2BC=4sqrt(7)-2sqrt(7)
2BC=2sqrt(7)
BC=sqrt(7)
⇒ AH=sqrt(7)+sqrt(7)=2sqrt(7).
По теореме Пифагора из △АСН: АС=sqrt((sqrt(21))^2+(2sqrt(7))^2)=sqrt(21+28)=sqrt(49)=7