Задача 8127 В трапеции ABCD боковая сторона AB...

Julia_Trusova

25.03.2016

В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD , если AD =14 , BC = 12 .

Так как AB⊥BC, то AB⊥AD(AD||BC)
EK⊥CD, EK-расстояние от Е до CD
AB⋂CD=M
CH-высота(CH⊥AD, CH||AB)
тогда, ABCH-прямоугольник
HD=AD-BC=14-12=2
Из △CHD: cos∠CDH=HD/CD=2/CD
Рассмотрим △BMC и △HCD:
∠MBC=∠CHD=90°; ∠BMC=∠HCD(как соответственные при параллельных прямых АВ и СН и секущей МD)
⇒△BMC ~ △HCD (по двум углам)
⇒MC/CD=BC/HD
MC/CD=12/2
MC=6CD
По теореме о касательной и секущей:
ME^2=MC*MD
ME^2=MC*(MC+CD)=6CD*(6CD+CD)=6CD*7CD=42CD^2
ME=sqrt(42*CD^2)=sqrt(42)*CD
Рассмотрим △MKE и △MAD:
∠EMK-общий, ∠MKE=∠MAD=90°
Тогда, ∠MEK=∠MDA (по теореме о сумме углов треугольника)
Значит, cos∠MEK=cos∠MDA=cos∠CDH
cos∠MEK=EK/ME
EK=ME*cos∠MEK=ME*cos∠CDH=2/CD*sqrt(42)*CD=2*sqrt(42)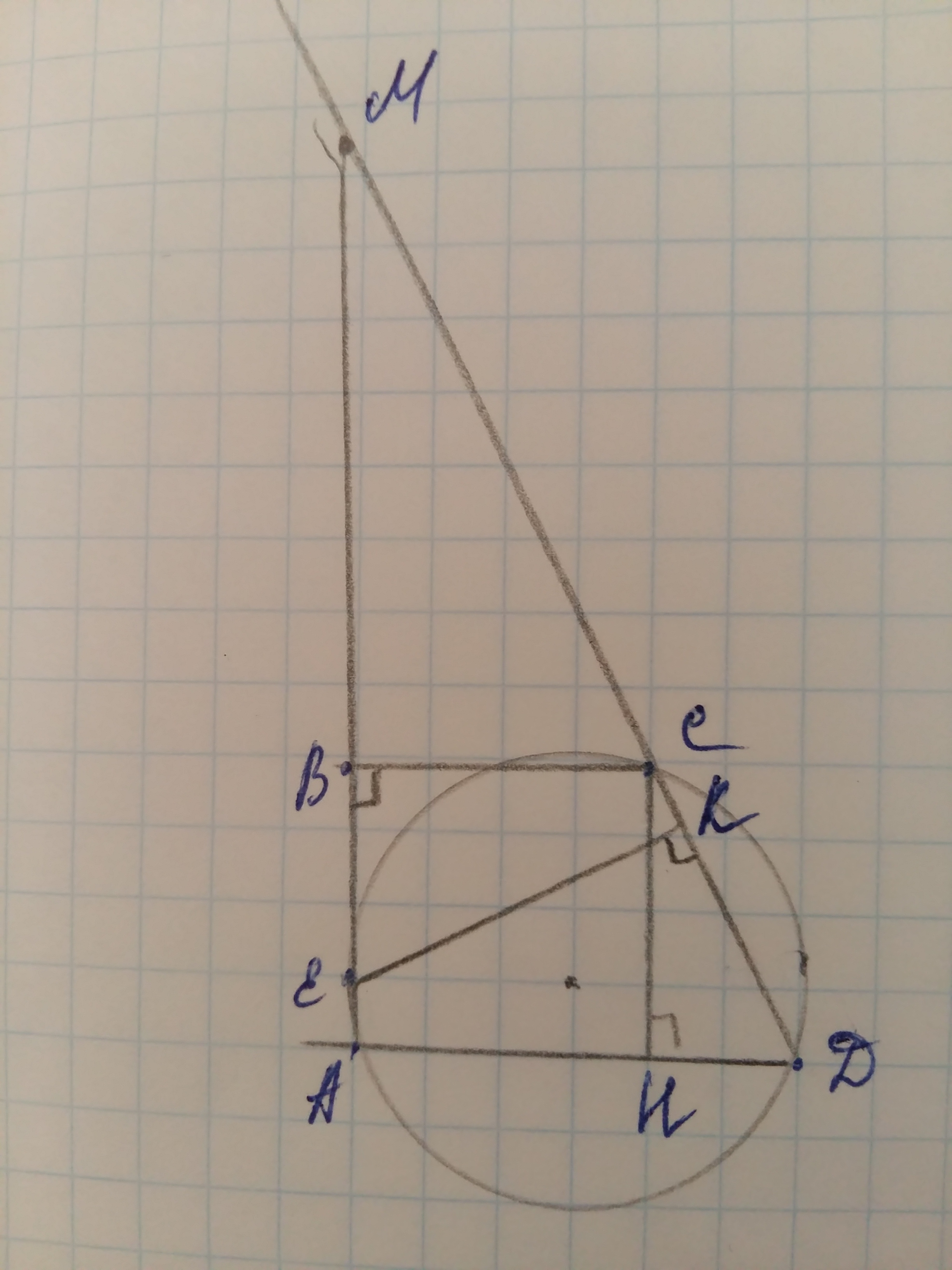

Ответ: 2*sqrt(42)