Задача 8096 Укажите неравенство, которое не имеет...

Julia_Trusova

24.03.2016

Укажите неравенство, которое не имеет решений.

1) x^2-56>0
2) x^2+56>0
3) x^2-56<0
4) x^2+56<0

1) x^2-56>0
Решим методом интервалов:
x^2-56=0
x^2=56
х=±sqrt(56)
х∈(-∞;-sqrt(56))⋃(sqrt(56);+∞) (Множество решений представлено на рисунке)
2) x^2+56>0
При любом значении х выражение принимает положительные значения(так как х^2⩾0 и если прибавить положительное число, в результате получится положительное число), значит
х∈(-∞;+∞)
3) x^2-56<0
Из решения первого неравенства следует, что решение данного неравенства:
х∈(-sqrt(56);+sqrt(56))
4) x^2+56<0
Так как выражение принимает только положительные значения(объяснение дано при решении второго неравенства), данное неравенство не имеет решений.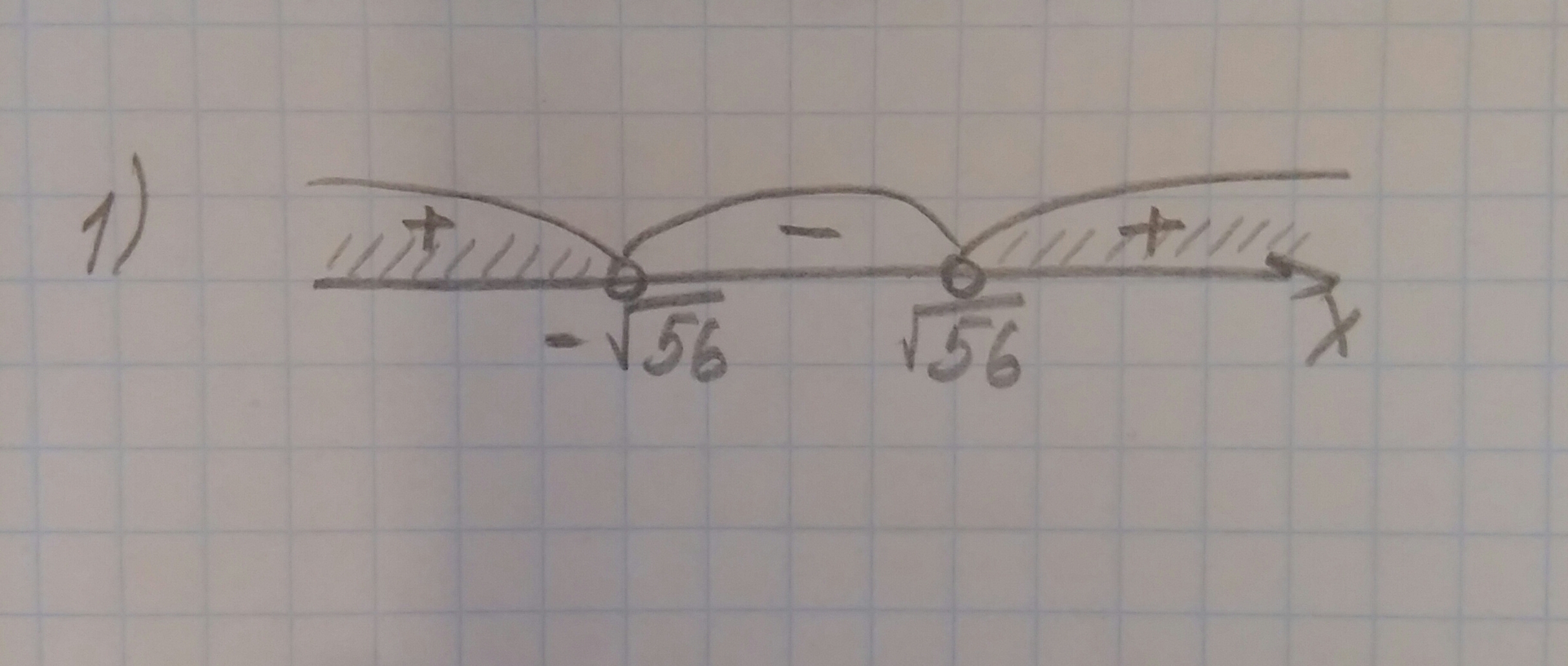

Ответ: 4