В равнобедренной трапеции ABCD основания ВС и AD равны 8 и 24 соответственно. Найдите расстояние от точки пересечения диагоналей трапеции до её большего основания,
если площадь трапеции равна 96
математика 8-9 класс
5003
Площадь трапеции вычисляется по формуле S=1/2(DC+AD)NK => 96=1/2(8+24)•NK => 16NK=96 => NK=6. ∆CNM∼∆AMK по двум углам (∠NMC=∠AMK как вертикальные, ∠BNM=∠AKM=90) => CN/AK=NM/MK, NM=6-MK => CN/AK=(6-MK)/MK => 4/12=(6-MK)/MK => 4MK=72-12MK => 16MK=72 => MK=4,5
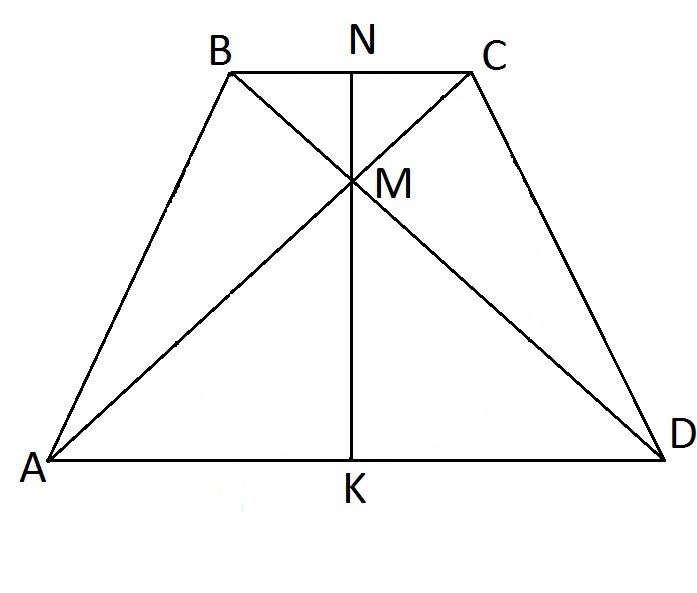
Ответ: 4,5
Ошибки в решение (2)
Площадь трапеции равна полу сумме оснований на высоту т.е. S=1/2(BC+AD)NK, а у вас вместо BC - DC
Равны будут углы < CNM и < AKM т.к. рассматриваются треугольники CNM и AMK

