Задача 80770 Не могу решить задачу 9 класс....
Условие

Решение
Отношение OB : ON = 8 : 5, AC = 20 см.
Найти периметр треугольника P(ABC).
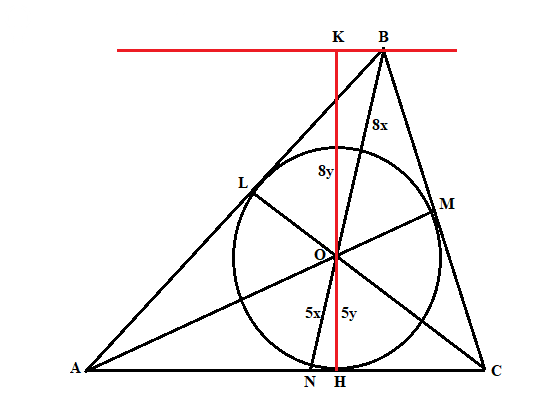
Обозначим OB = 8x, ON = 5x.
Сделаем несколько дополнительных построений,
они показаны красным цветом. KB || AC, KH ⊥ AC.
Точка пересечения биссектрис O - центр вписанной окружности.
Через эту точку О проводим высоту KH длиной h.
Треугольники ONH и OBK подобны друг другу.
Это значит, что OK : OH = OB : ON = 8 : 5.
Обозначим OK = 8y, OH = 5y, тогда KH = 13y
Но с другой стороны, OH = r - радиусу вписанной окружности.
Получаем: h : r = 13 : 5, то есть h = 13/5*r
Есть две формулы площади треугольника:
1) [m]\large S(Δ) = \frac{a \cdot h}{2} = \frac{AB \cdot h}{2} = \frac{20h}{2} = 10h = 10 \cdot \frac{13}{5} \cdot r = 26r[/m]
2) [m]\large S(Δ) = \frac{P \cdot r}{2}[/m], отсюда:
[m]\large P = \frac{2 \cdot S}{r} = \frac{2 \cdot 26r}{r} = 52[/m]
Есть второй способ, для тех, кто не знает 2) формулу площади треугольника или лень делать дополнительные построения.
Есть такое свойство биссектрисы угла в треугольнике:
Биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Рассмотрим треугольник ABN. Биссектриса AO угла А делит противоположную сторону BN на отрезки BO = 8x и ON = 5x.
Значит, прилежащие стороны относятся друг к другу так же:
AB : AN = BO : ON = 8 : 5. Отсюда AB = AN*8/5
Теперь рассмотрим треугольник BCN. Биссектриса СO угла С делит противоположную сторону BN на отрезки BO = 8x и ON = 5x.
BC : NC = BO : ON = 8 : 5. Отсюда BC = NC*8/5
Находим периметр треугольника:
P = AB + BC + AC = AN*8/5 + NC*8/5 + AC = 8/5*(AN + NC) + AC =
= 8/5*AC + AC = 8/5*20 + 20 = 32 + 20 = 52
P = 52
Ответ получился точно такой же.
Ответ: 52