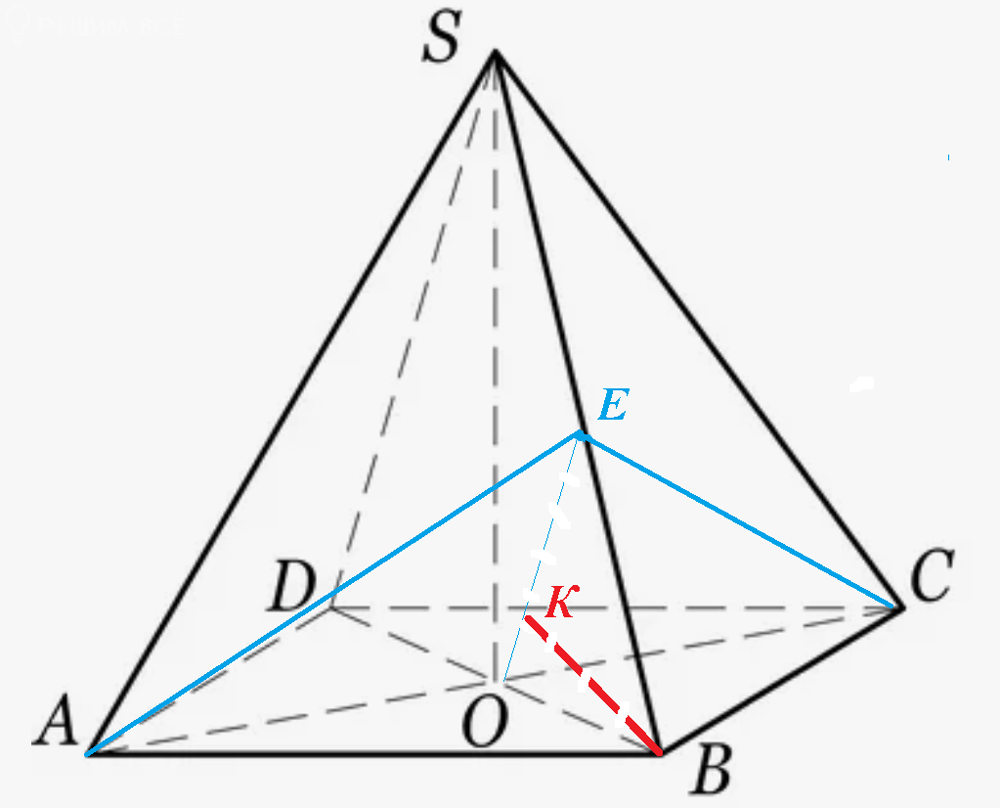
Задача 80767 4. В правильной четырехугольной пирамиде...

698f4c6f0181c00556c1ccad

2/13/2026 4:08:47 PM

4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка E- середина ребра SB. Найдите расстояние от точки В до плоскости АСЕ.

5f3ea7e3faf909182968ddd9

2/14/2026 7:38:14 AM

★

Искомое расстояние это высота треугольника ОВЕ

AE=CE=sqrt(3)/2 - высоты равносторонних треугольников ASB и BSC
AC=sqrt(2)- диагональ квадрата АВСD

Δ АСЕ - равнобедренный

ОE=1/2

Δ ОВЕ - равнобедренный
OE=BE=1/2 ( Е- середина SB)
OB=sqrt(2)/2 - половина диагонали квадрата

S_( Δ ОВЕ)=(1/2)*ОВ* h ( h=sqrt((1/2)^2-(sqrt(2)/4))^2)=sqrt(2)/4

S_( Δ ОВЕ)=(1/2)*(sqrt(2)/2)*(sqrt(2)/4)=1/8

S_( Δ ОВЕ)=(1/2)*ОЕ*ВК ⇒ [b]ВК= (1/2)[/b]

О т в е т. 1/2


Координатный метод:

Ответ от нейросети
Расположим пирамиду в прямоугольной системе координат.
Пусть основание ABCD – квадрат со стороной 1, лежащий в плоскости z = 0, а его центр O — начало координат:

A (-½,-½,0) , B (½,-½,0) , C (½,½,0) , D (-½,½,0).

В правильной пирамиде боковые ребра равны сторонам основания, поэтому вершина S находится на оси, проходящей через O, на высоте h, где

SA² = (½)² + (½)² + h² = 1
⇒ h² = 1 – ½ = ½ ⇒ h = 1/√2,

то есть S (0,0,1/√2).

Точка E – середина SB:

E ( (½+0)/2 , (-½+0)/2 , (0+1/√2)/2 ) = (¼, –¼, 1/(2√2) ).

Найдём расстояние от точки B до плоскости ACE.
Возьмём векторы

AC = C – A = (1, 1, 0),
AE = E – A = (¾, ¼, 1/(2√2)).

Нормальный вектор к плоскости ACE:

n = AC × AE = (h/2, –h/2, –½) = (1/(2√2), –1/(2√2), –½).

Вектор AB:

B – A = (1, 0, 0).

Расстояние d от точки B до плоскости ACE:

d = |(B – A) · n| / |n|
= |1 · (1/(2√2))| / √[(1/(2√2))² + (-1/(2√2))² + (-½)²]
= (1/(2√2)) / √(1/8 + 1/8 + 1/4)
= (1/(2√2)) / √(1/2)
= (1/(2√2)) · (√2)
= 1/2.

Ответ: 1/2.