Задача 80764 Вариант № 76222984 1. Найдите значение...
Условие
1. Найдите значение c по графику функции [m] y = ax^2 + bx + c [/m], изображенному на рисунке.
Варианты ответа
1. 4
2. -5
3. 5
4. 12
2. Найдите значение a по графику функции [m] y = ax^2 + bx + c [/m], изображенному на рисунке.
3. Найдите значение b по графику функции [m] y = ax^2 + bx + c [/m], изображенному на рисунке.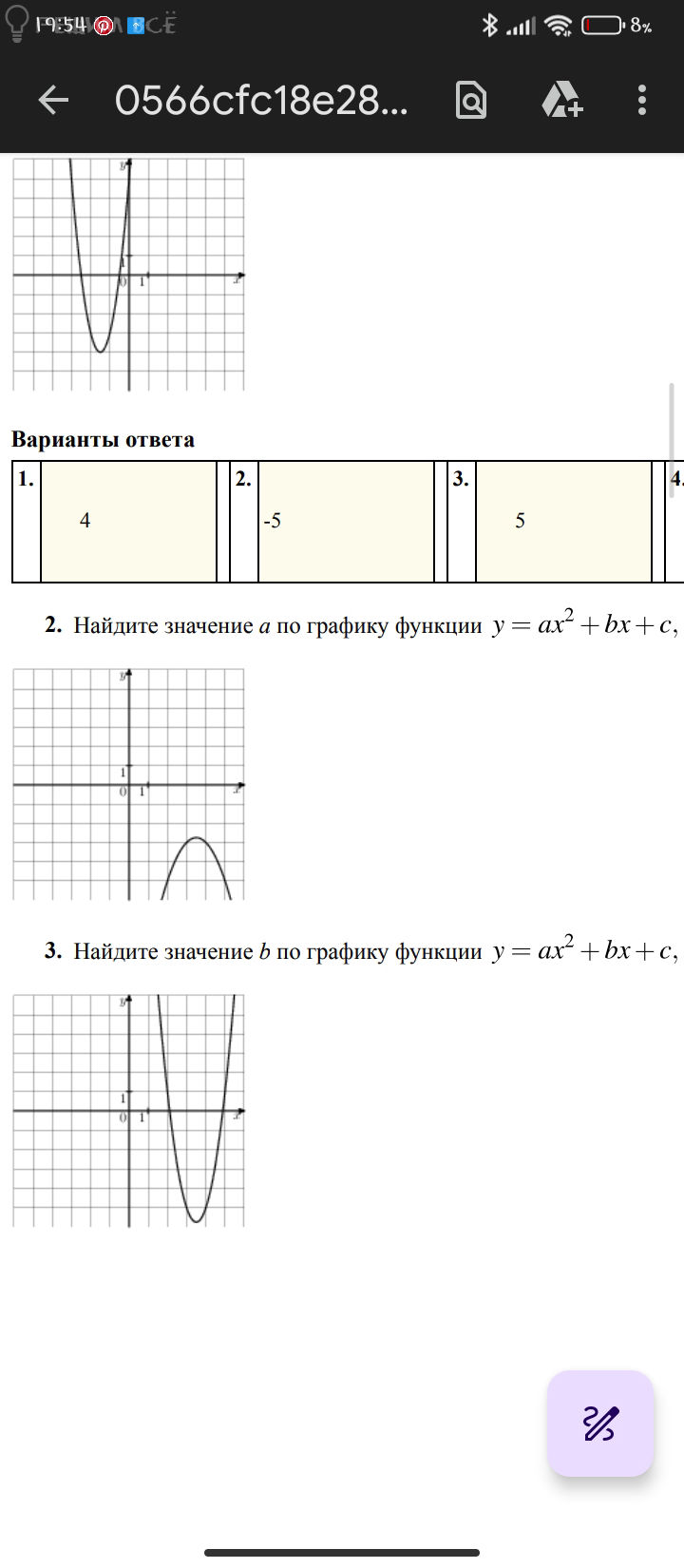
Решение
Коэффициент a определяет направление ветвей и крутизну графика.
Коэффициент b определяет положение вершины. x0 = -b/(2a).
Свободный член c определяет точку пересечения с осью Oy.
1) Мы видим, что график пересекается с осью Oy в точке y = 5.
Значит, [b]c = 5[/b]
2) Мы видим, что ветви параболы направлены вниз, значит, a < 0.
Парабола проходит через точку: (5; -5)
При этом вершина находится в точке (3,5; -2,75)
При смещении на 1 по оси Ox мы получаем смещение на 2 по оси Oy.
x0 = -b/(2a) = 3,5
b = -7a
Подставляем в уравнение:
{ a*3,5^2 - 7a*3,5 + с = -2,75
{ a*5^2 - 7a*5 + c = -5
Считаем:
{ 12,25a - 24,5a + c = -2,75
{ 25a - 35a + c = -5
Выразим c через а во 2 уравнении и подставим в 1 уравнение:
{ c = 10a - 5
{ -12,25a + 10a - 5 = -2,75
Получаем:
-2,25a = 2,25
[b]a = -1[/b]
3) Ветви направлены вверх, значит, a > 0.
Вершина находится в точке (3,5; -6),
x0 = -b/(2a) = 3,5
b = -7a
a*3,5^2 + b*3,5 + c = -6
Парабола проходит через точку (4; -5).
a*4^2 + b*4 + c = -5
Составляем систему:
{ 12,25a - 7a*3,5 + c = -6
{ 16a - 7a*4 + c = -5
Считаем:
{ 12,25a - 24,5a + c = -6
{ 16a - 28a + c = -5
Выразим с через а во 2 уравнении и подставим в 1 уравнение:
{ c = 12a - 5
{ -12,25a + 12a - 5 = -6
Получаем:
-0,25a = -1
a = -1/(-0,25) = 4
b = -7a = -7*4
[b]b = -28[/b]