Задача 80759 Помогите решить геометрию(кроме 3)...
Условие

Решение
TK - средняя линия ΔMPN, |TK| = |MP|/2 = 10/2 = 5 см
BK - средняя линия ΔFNP, |BK| = |FN|/2 = 16/2 = 8 см
AT - средняя линия ΔFNM, |AT| = |FN|/2 = 16/2 = 8 см
ABKT - параллелограмм.
P(ABKT) = 2*5 + 2*8 = 10 + 16 = 26 см
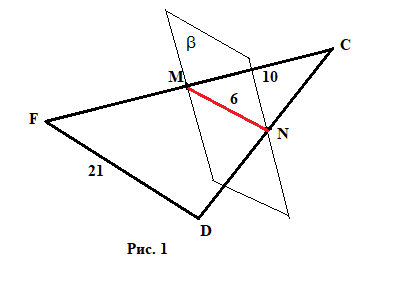
2) MN = 6 см, FD = 21 см, MC = 10 см
Смотрите Рис. 1.
По теореме Фалеса:
[m]\large \frac{FC}{MC} = \frac{FD}{MN}[/m]
[m]\large \frac{FC}{10} = \frac{21}{6}[/m]
[m]FC = \frac{21 \cdot 10}{6} = \frac{7 \cdot 3 \cdot 2 \cdot 5}{2 \cdot 3} = 7 \cdot 5 = 35[/m]
3) Изображением центра описанной окружности будет опять центр описанной окружности нового треугольника.
Это точка пересечения серединных перпендикуляров к сторонам.
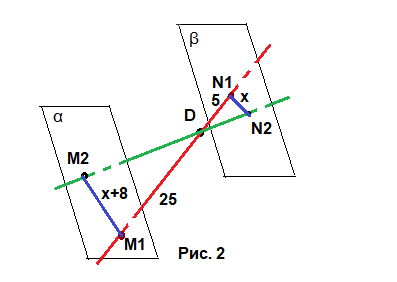
4) Смотрите Рис. 2.
Если M1N1 = 30 см, а DN1 = 5 см, то DM1 = 30 - 5 = 25 см.
Обозначим длину N1N2 = x см, тогда длина M1M2 = x+8 см.
Треугольники DN1N2 и DM1M2 подобны друг другу.
Коэффициент подобия:
[m]k = \frac{DM1}{DN1} = \frac{25}{5} = 5[/m]
Тогда:
[m]\frac{M1M2}{N1N2} = k[/m]
[m]\frac{x+8}{x} = 5[/m]
[m]x+8 = 5x[/m]
[m]x = 2[/m] см
[m]x+8 = 10[/m] см
Ответ: 10 см
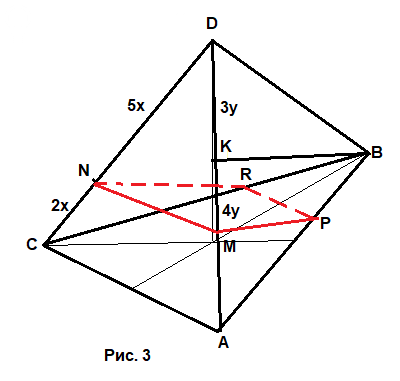
6) Смотрите Рис. 3
Обозначим DN = 5x, CN = 2x, DK = 3y, CK = 4y.
Так как плоскость сечения параллельна AC, то очевидно, на грани ACD нужно провести прямую параллельную AC:
NM || AC.
Так как плоскость сечения параллельна BK, то очевидно, на грани ABD нужно провести прямую параллельную BK:
MP || BK.
Так как плоскость сечения параллельна AC, то очевидно, на грани ABC нужно провести прямую параллельную AC:
PR || AC.
И после этого остается провести прямую RN.
По теореме Фалеса:
[m]\large \frac{DM}{MA} = \frac{DN}{NC} = \frac{5}{2}[/m]
Поэтому DK = 3y, KM = 2y, MA = 2y.
Тогда получается, что MP проходит через середину отрезка AK и MP || BK.
Это означает, что MP - средняя линия ΔABK.
Значит, точка P - середина стороны AB. И при этом PR || AC.
Это в свою очередь означает, что PR - средняя линия ΔABC.
То есть точка R делит отрезок BC пополам, то есть в отношении 1:1.
Ответ: Сечение делит BC в отношении 1:1.