Задача 80744 решить подробно 2 задачи и написать...
Условие

Решение
[m]f(x) = f(0) + \frac{f'(0)}{1!} \cdot x + \frac{f''(0)}{2!} \cdot x^2 + ... + \frac{f^{(n)}(0)}{n!} \cdot x^{n} + ...[/m]
В нашем случае f(x) = x^2 cos 2x
f(0) = 0^2*cos 0 = 0
f'(x) = 2x cos 2x + x^2(-2sin 2x) = 2x cos 2x - 2x^2 sin 2x
f'(0) = 2*0*cos 0 - 2*0*sin 0 = 0
f''(x) = 2cos 2x + 2x(-2sin 2x) - 4x sin 2x - 2x^2*2cos 2x =
= 2cos 2x - 8x sin 2x - 4x^2 cos 2x
f''(0) = 2cos 0 - 8*0*sin 0 - 4*0*cos 0 = 2*1 - 0 - 0 = 2
f'''(x) = 4(-sin 2x) - 8sin 2x - 16x cos 2x - 8x cos 2x + 8x^2 sin 2x =
= -12sin 2x - 24x cos 2x + 8x^2 sin 2x
f'''(0) = -12*sin 0 - 24*0*cos 0 + 8*0*sin 0 = 0
f^((4))(x) = -24cos 2x - 24cos 2x + 48x sin 2x + 16x sin 2x + 16x^2 cos 2x =
= -48cos 2x + 64x sin 2x + 16x^2 cos 2x
f^((4))(0) = -48cos 0 + 64*0*sin 0 + 16*0*cos 0 = -48*1 + 0 + 0 = -48
f^((5))(x) = 96sin 2x + 64sin 2x + 128x cos 2x + 32x cos 2x - 32x^2 sin 2x =
= 160sin 2x + 160x cos 2x - 32x^2 sin 2x
f^((5))(0) = 160sin 0 + 160*0*cos 0 - 32*0*sin 0 = 0 + 0 + 0 = 0
f^((6))(x) =320cos 2x + 160cos 2x - 320x sin 2x - 64x sin 2x - 64x^2 cos 2x=
= 480cos 2x - 384x sin 2x - 64x^2 cos 2x
f^((6))(0) = 480cos 0 - 384*0*sin 0 - 64*0*cos 0 = 480*1 + 0 + 0 = 480
f^((7))(x) =-960sin 2x-384sin 2x - 768x cos 2x - 128x cos 2x + 128x^2 sin 2x=
= -1344sin 2x - 896x cos 2x + 128x^2 sin 2x
f^((7))(0) = -1344*sin 0 - 896*0*cos 0 + 128*0*sin 0 = -0 - 0 + 0 = 0
И так далее. Ряд Маклорена получается такой:
[m]x^2 \cos 2x = \frac{f''(0)}{2!} \cdot x^2 + \frac{f^{(4)}(0)}{4!} \cdot x^4 + \frac{f^{(6)}(0)}{6!} \cdot x^6 + ...[/m]
[m]x^2 \cos 2x = \frac{2}{2} \cdot x^2 - \frac{48}{24} \cdot x^4 + \frac{480}{720} \cdot x^6 - ... = x^2 - 2x^4 + \frac{2}{3} \cdot x^6 - ...[/m]
Ответ: Ряд Маклорена: x^2 cos 2x = x^2 - 2x^4 + 2/3*x^6 - ...
f^((6))(0) = 480; f^((7))(x) = -1344sin 2x - 896x cos 2x + 128x^2 sin 2x
Задача 4. Исследовать функцию и построить график.
а) [m]y(x) = \frac{1}{x} + 4x^2 = \frac{1 + 4x^3}{x}[/m]
Схема исследования функции:
1. Найти область определения. Выделить особые точки (точки разрыва).
x ≠ 0, x ∈ (-oo; 0) U (0; +oo).
В точке x = 0 неустранимый разрыв 2 рода - уход в бесконеч-ность.
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Вертикальная асимптота x = 0, то есть ось Oy.
3. Найти точки пересечения с осями координат и промежутки знакопостоянства.
С осью Oy пересечения нет.
Пересечение с осью Ox, y(x) = 0
1 + 4x^3 = 0
x^3 = -1/4 = -2/8
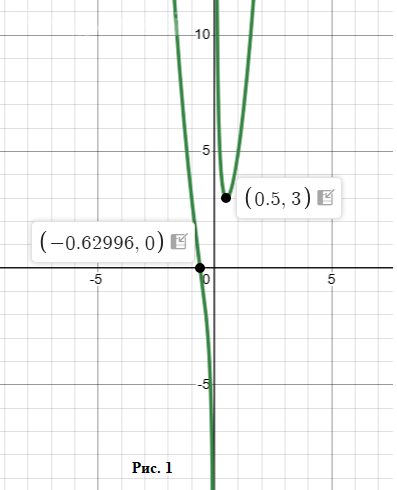
[m]x = -\frac{\sqrt[3]{2}}{2} ≈ -0,63[/m]
4. Определить, является ли функция чётной или нечётной.
Не четная и не нечетная.
5. Определить, является ли функция периодической.
Не периодическая.
6. Найти точки экстремума и интервалы возрастания-убывания.
Точки экстремума - это точки, в которых y' = 0 или не существует.
[m]y'(x) = \frac{12x^2 \cdot x - (1+4x^3)}{x^2} = \frac{8x^3 - 1}{x^2} = 0[/m]
8x^3 - 1 = 0
x^3 = 1/8
[b]x = 1/2[/b]
При x < 0 будет y' < 0 - функция убывает.
При x ∈ (0; 1/2) будет y' < 0 - функция убывает.
При x > 1/2 будет y' > 0 - функция возрастает.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
Точки перегиба - это точки, в которых y'' = 0 или не существует.
[m]y''(x) = \Bigg ( \frac{8x^3 - 1}{x^2} \Bigg )' =0[/m]
[m] \frac{24x^2 \cdot x^2 - (8x^3 - 1) \cdot 2x}{x^4} = \frac{24x^3 - 2(8x^3 - 1)}{x^3} = \frac{8x^3 +1}{x^3} = 0[/m]
8x^3 + 1 = 0
[b]x = -1/2[/b]
При x < -1/2 будет y'' > 0 - график вогнутый (выпуклый вниз).
При x ∈ (-1/2; 0) будет y'' < 0 - график выпуклый (выпуклый вверх).
При x > 0 будет y'' > 0 - график вогнутый (выпуклый вниз).
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Наклонная асимптота имеет вид: f(x) = kx + b, где:
[m]k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} \frac{1 + 4x^3}{x^2} = \lim \limits_{x \to \infty} \frac{1/x^3 + 4}{x^2/x^3} = \frac{0 + 4}{0} = \infty[/m]
Наклонных и горизонтальных асимптот нет.
9. Выбрать дополнительные точки и вычислить их координаты (при необходимости).
[m]y(\frac{1}{2}) = \frac{1 + 4 \cdot 1/8}{1/2} = 2(1 + \frac{1}{2}) = 3[/m]
A(1/2; 3) - точка минимума.
[m]y(-\frac{1}{2}) = \frac{1 + 4 \cdot (-1/8)}{-1/2} = -2(1 - \frac{1}{2}) = -1[/m]
B(-1/2; -1) - точка перегиба.
10. Построить график функции, ее асимптот, отметить ключевые точки.
График показан на рисунке 1.
б) [m]y(x) = \ln (\sin x - \cos x)[/m]
Схема исследования функции:
1. Найти область определения. Выделить особые точки (точки разрыва).
sin x - cos x > 0
sin x > cos x
tg x > 1
[b]x ∈ (π/4 + π*k; π/2 + π*k), k ∈ Z[/b]
Это точки неустранимых разрывов 2 рода (уход в бекнеч-ность).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Вертикальные асимптоты при:
sin x - cos x = 0
sin x = cos x
tg x = 1
x = π/4 + π*k, k ∈ Z
Рассмотрим пределы в двух точках π/4 и -3π/4:
[m]\lim \limits_{x \to \pi/4} = \ln (\sin x - \cos x) = \ln (\sin \pi/4 - \cos \pi/4) =[/m]
[m]= \ln (\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}) = \ln 0 = -\infty[/m]
[m]\lim \limits_{x \to -3\pi/4} = \ln (\sin x - \cos x) = \ln (\sin (-3\pi/4) - \cos (-3\pi/4)) = [/m]
[m]= \ln (-\frac{\sqrt{2}}{2} - (-\frac{\sqrt{2}}{2})) = \ln 0 = -\infty[/m]
3. Найти точки пересечения с осями координат и промежутки знакопостоянства.
При x = 0 будет:
[m]y(0) = \ln (\sin 0 - \cos 0) = \ln (0 - 1) = \ln(-1)[/m] - не определено.
С осью Oy пересечения нет
Пересечения с осью Ox.
[m]\ln (\sin x - \cos x) = 0[/m]
[m]\sin x - \cos x = 1[/m]
Это бывает в двух случаях:
1) [m]\begin{cases}
\sin x = 1 \\
\cos x = 0 \\
\end{cases}[/m]
[b]x1 = π/2 + 2π*n, n ∈ Z[/b]
2) [m]\begin{cases}
\sin x = 0 \\
\cos x = -1 \\
\end{cases}[/m]
[b]x2 = π + 2π*n, n ∈ Z[/b]
4. Определить, является ли функция чётной или нечётной.
Не четная и не нечетная.
5. Определить, является ли функция периодической.
Периодическая. Период [b]T = 2π[/b], как у функций sin x и cos x.
6. Найти точки экстремума и интервалы возрастания-убывания.
Точки экстремума - это точки, в которых y' = 0 или не существует.
[m]y' = \frac{\cos x - (-\sin x)}{\sin x - \cos x} = 0[/m]
[m]\frac{\cos x + \sin x}{\sin x - \cos x} = 0[/m]
cos x + sin x = 0
sin x = -cos x
tg x = -1
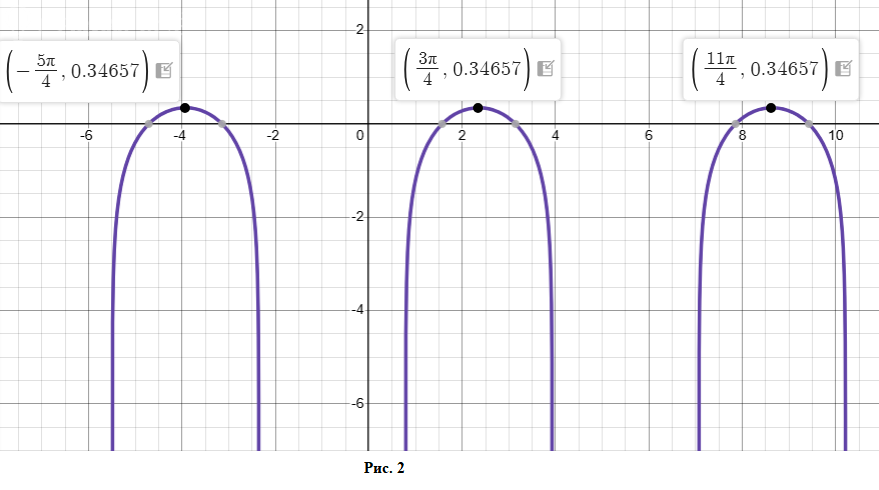
[b]x = 3π/4 + π*m, m ∈ Z[/b]
Это всегда точки максимума,
потому что в точках разрыва функция уходит в минус бесконеч-ность.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
Точки перегиба - это точки, в которых y'' = 0 или не существует.
[m]y''(x) = \Bigg ( \frac{\sin x + \cos x}{\sin x - \cos x}\Bigg )' =0[/m]
[m] \frac{(\cos x - \sin x)(\sin x - \cos x) - (\sin x + \cos x)(\cos x + \sin x)}{(\sin x - \cos x)^2} =0[/m]
-(cos x - sin x)^2 - (sin x + cos x)^2 = 0
-(cos^2 x - 2sin x*cos x + sin^2 x) - (cos^2 x + 2sin x*cos x + sin^2 x) = 0
-(1 - 2sin x*cos x) - (1 + 2sin x*cos x) = 0
-1 + 2sin x*cos x - 1 - 2sin x*cos x = 0
-2 = 0
Это уравнение всегда ложно, значит, точек перегиба нет.
Так как у функции y''(x) числитель равен -2, а в знаменателе квадрат, то
y'' < 0 при любом x из области определения.
Значит, график точек перегиба не имеет.
При всех x график выпуклый (выпуклый вверх).
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Наклонных и горизонтальных асимптот нет.
9. Выбрать дополнительные точки и вычислить их координаты (при необходимости).
Дополнительных точек нет.
10. Построить график функции, ее асимптот, отметить ключевые точки.
График показан на рисунке 2.