Задача 80740 решить, и написать что нужно найти...
Условие
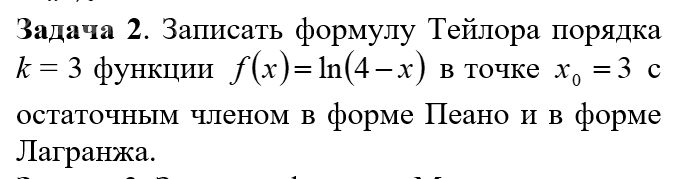
Решение
Для функции
f(x)=ln(4−x), x₀=3, k=3
нужно записать её разложение в ряд Тейлора порядка 3:
f(x)=T₃(x)+R₃(x), T₃(x)=∑_{n=0}^{3} f^{(n)}(x₀) (x−x₀)^{n}/n!,
а остаточный член R₃(x) –
• в форме Пеано: o((x−x₀)³),
• в форме Лагранжа: f^{(4)}(ξ)(x−x₀)⁴/4!, ξ∈(x,x₀).
Решение.
1. Производные в точке x₀=3.
f(x)=ln(4−x)
f′(x)=−1/(4−x) ⇒ f′(3)=−1
f″(x)=1/(4−x)² ⇒ f″(3)=1
f‴(x)=2/(4−x)³ ⇒ f‴(3)=2
2. Тейлоров многочлен 3-го порядка:
T₃(x)=f(3)+f′(3)(x−3)+f″(3)(x−3)²/2!+f‴(3)(x−3)³/3!
=0−(x−3)+(x−3)²/2+(x−3)³/3.
3. Остаточный член.
а) Форма Пеано:
f(x)=−(x−3)+(x−3)²/2+(x−3)³/3+o((x−3)³), x→3.
б) Форма Лагранжа. Для этого нужна 4-я производная:
f⁽⁴⁾(x)=6/(4−x)⁴.
Тогда
R₃(x)=f⁽⁴⁾(ξ) (x−3)⁴/4!= 6/(4−ξ)⁴ · (x−3)⁴/24
= (x−3)⁴ / [4(4−ξ)⁴], ξ∈(x,3).
Ответ.
f(x)=ln(4−x)=−(x−3)+ (x−3)²/2 + (x−3)³/3 + o((x−3)³), x→3
или, с остатком Лагранжа,
f(x)=−(x−3)+ (x−3)²/2 + (x−3)³/3 + (x−3)⁴ / [4(4−ξ)⁴], ξ∈(x,3).
Все решения
[m]f(x) = f(x0) + \frac{f'(x0)}{1!} \cdot (x - x0) + \frac{f''(x0)}{2!} \cdot (x - x0)^2 +[/m]
[m]+ \frac{f'''(x0)}{3!} \cdot (x - x0)^3 + R_4(x)[/m]
R_(4)(x) - это и есть остаточный член.
В форме Лагранжа он выглядит, почти как следующий член ряда:
[m]R_4(x) = \frac{f^{(4)}(x0 + θ \cdot (x-x0) )}{4!} \cdot (x - x0)^4[/m]
Где θ ∈ (0; 1) - это малая добавка, умноженная на (x - x0).
В форме Пеано остаточный член выглядит так:
[m]R_4(x) = \overline{o}(x - x0)^4[/m]
Теперь найдем все производные:
[m]f(x) = \ln (4 - x)[/m]
[m]f'(x) = -\frac{1}{4-x}[/m]
[m]f''(x) = -(\frac{1'(4-x)-1(4-x)'}{(4-x)^2}) = -(\frac{0-1(-1)}{(4-x)^2}) = -\frac{1}{(4-x)^2}[/m]
[m]f''' = -\frac{1'(4-x)^2 - 1((4-x)^2)'(4-x)'}{(4-x)^4} = -\frac{0 - 2(4-x)(-1)}{(4-x)^4} = -\frac{2}{(4-x)^3}[/m]
[m]f^{(4)} = -\frac{2'(4-x)^3 - 2((4-x)^3)'(4-x)'}{(4-x)^6} = -\frac{0 - 2 \cdot 3(4-x)^2(-1)}{(4-x)^6} = -\frac{6}{(4-x)^4}[/m]
Формула Тейлора с остаточным членом Лагранжа:
[m]f(x) = \ln(4 - x0) - \frac{1}{1(4-x0)} \cdot (x - x0) - \frac{1}{2(4-x0)^2} \cdot (x - x0)^2 - [/m]
[m]- \frac{2}{6(4-x0)^3} \cdot (x - x0)^3 - \frac{6}{24(4-x0 - θ \cdot (x-x0))^4} \cdot (x - x0)^4[/m]
Можно сократить дроби:
[m]f(x) = \ln(4 - x0) - \frac{x - x0}{4-x0} - \frac{(x - x0)^2}{2(4-x0)^2} - \frac{(x - x0)^3}{3(4-x0)^3} - \frac{(x - x0)^4}{4(4-x0 - θ \cdot (x-x0))^4}[/m]
Формула Тейлора с остаточным членом Пеано:
[m]f(x) = \ln(4 - x0) -\frac{x - x0}{4-x0} - \frac{(x - x0)^2}{2(4-x0)^2} - \frac{(x - x0)^3}{3(4-x0)^3} + \overline{o}(x - x0)^4[/m]