Задача 80739 Помогите пожалуйста решить...
Условие

Решение
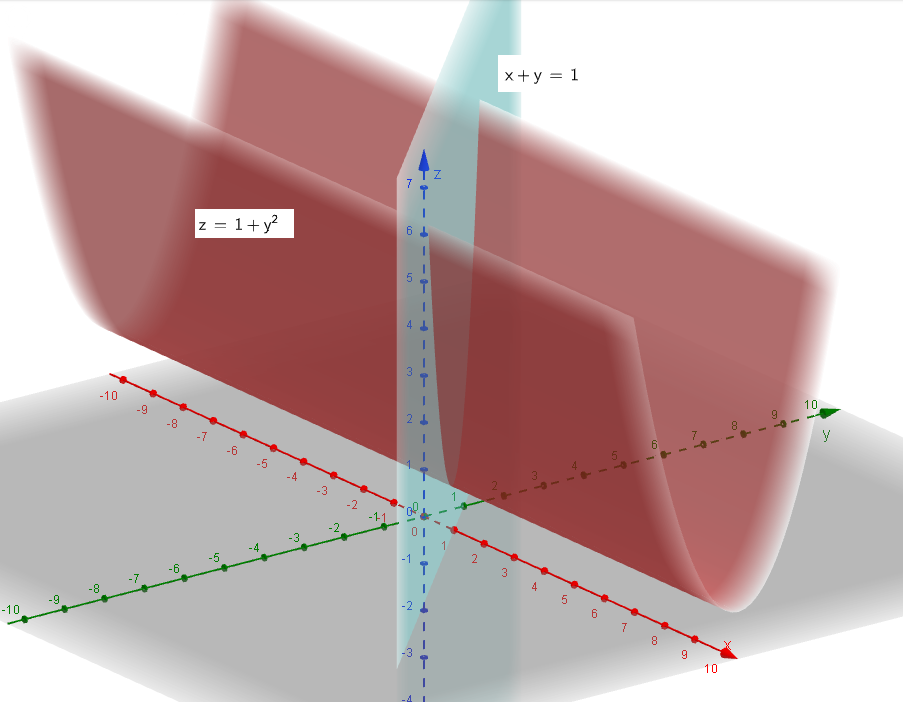
x+y=1 - плоскость, параллельная оси Ох
[b]Через тройной интеграл:[/b]
[m] V= ∫ ∫ ∫_{ Ω } dxdydz[/m]
Ω :
0 ≤ x ≤ 1
0 ≤ y ≤ 1-x
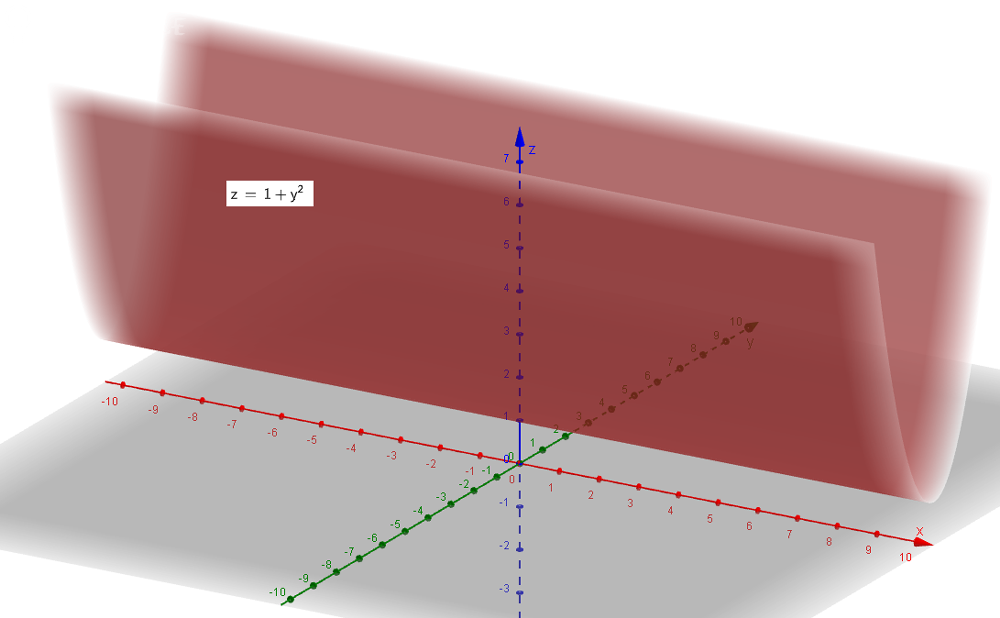
0 ≤ z ≤ 1+y^2
[m] V= ∫ ∫_{ Ω } dxdydz=∫^{1}_{0} ( ∫^{1-x} _{0}(z)|^{1+y^2}_{0}dy)dx= [/m]
далее счет такой же как при вычислении объема через двойной интеграл
[b]Через двойной интеграл:[/b]
[m] V= ∫ ∫ _{D} (1+y^2)dxdy[/m]
D:
0 ≤ x ≤ 1
0 ≤ y ≤ 1-x
[m]V = ∫^{1}_{0} ( ∫^{1-x} _{0} (1+y^2)dy)dx=∫^{1}_{0}(y+\frac{y^3}{3})|^{1-x} _{0} dx=∫^{1}_{0}(1-x+\frac{(1-x)^3}{3})dx=(x-\frac{x^2}{2}-\frac{1}{3}\cdot \frac{(1-x)^4}{4})|^{1}_{0}=[/m]
[m] =1-\frac{1}{2}-\frac{1}{12}\cdot 0 -0-0+\frac{1}{12}=\frac{7}{12}[/m]