Задача 80738 ...

6977a6ebca02e81d6ad1c8cb

1/26/2026 5:42:48 PM

Решение и начертить1. Точки K, E, и O лежат на прямой, перпендикулярной к плоскости α, а точки O, B, A и M лежат в плоскости α. Какие из следующих углов являются прямыми: ∠MOK, ∠OKB и ∠AOE.

2. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны √24, 8 и 9.

3. В прямоугольном параллелепипеде ABCDA1B1C1D1 проведены диагонали B1D и B1C. Построить (найти) линейный угол двугранного угла ∠B1DCB.

4. Отрезок CD1 к плоскости прямоугольного ∆ABC, где ∠B=90°. Определить вид ∆ABD.

5. Прямая BD перпендикулярна к плоскости ∆ABC. Известно, что BD=9 см, AC=10 см, BC=BD=13 см. Найдите расстояние от точки D до прямой AC.

626fab9a354ab65fb2f43abb

1/27/2026 11:48:09 AM

★

1. Точки K, E, и O лежат на прямой, перпендикулярной к плоскости α, а точки O, B, A и M лежат в плоскости α. Какие из следующих углов являются прямыми: ∠MOK, ∠OKB и ∠AOE.
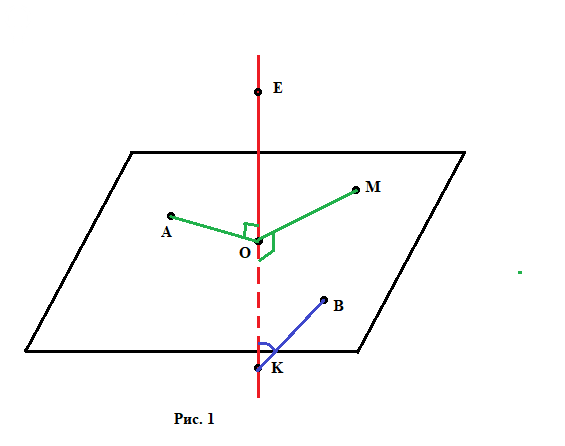
Точка О, очевидно, лежит и на прямой, и в плоскости.
То есть это точка пересечения плоскости и перпендикулярной к ней прямой.
Поэтому, если в середине названия угла стоит букв О, то он прямой.
Смотрите Рис. 1
∠MOK и ∠AOE - точно прямые (зеленые). ∠OKB - нет (синий).
Ответ: ∠MOK и ∠AOE.

2. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны √24, 8 и 9.
Это очень просто:
[m]D = \sqrt{a^2+b^2+c^2} = \sqrt{24+8^2+9^2} =[/m]
[m] = \sqrt{24+64+81}= \sqrt{169} = 13[/m]
Ответ: D = 13

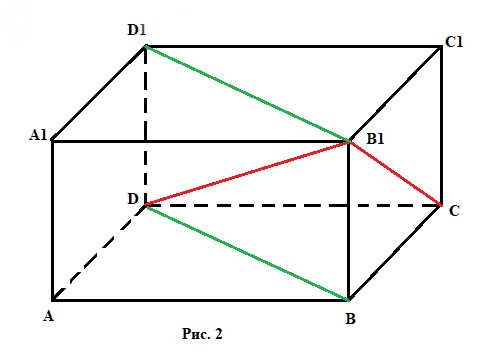
3. В прямоугольном параллелепипеде ABCDA1B1C1D1 проведены диагонали B1D и B1C. Построить (найти) линейный угол двугранного угла ∠B1DCB.
Как я понял, этот двугранный угол - это угол между треугольниками
ΔBB1D и ΔBB1C
Это угол между гранью BB1C1C и диагональным сечением BB1D1D.
Смотрите Рис. 2.
Сечение BB1D1D показано зеленым, диагонали B1D и B1C - красным.
Ответ: Линейный угол двугранного угла равен углу CBD.

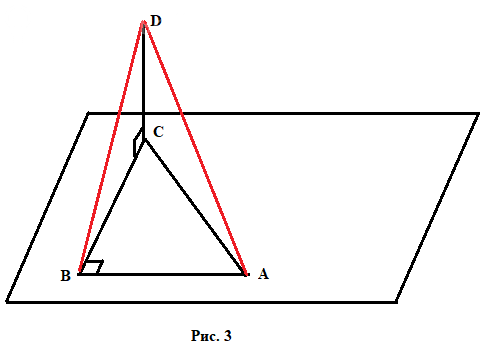
4. Отрезок CD ⊥ к плоскости прямоугольного ∆ABC, где ∠B=90°. Определить вид ∆ABD.
Смотрите Рис. 3.
Отрезки AD и BD я достроил красным.
Если ∠ ABC = 90° и ∠ BCD = 90°, то и ∠ ABD = 90°.
Кажется, это по теореме о трех перпендикулярах, хотя я не уверен.
Ответ: ∆ABD - прямоугольный.

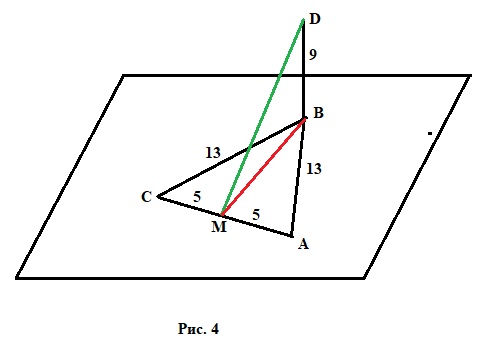
5. Прямая BD перпендикулярна к плоскости ∆ABC. Известно, что BD=9 см, AC=10 см, BC=BA=13 см. Найдите расстояние от точки D до прямой AC.
Смотрите Рис. 4. Расстояние от т. D до (AC) это DM, показано зеленым.
Так как ABC - равнобедренный треугольник с вершиной B, то
BM - медиана, она же высота и биссектриса, показана красным.
AC = 10, поэтому AM = CM = 5.
Треугольник ΔABM - прямоугольный, BM из теоремы Пифагора:
[m]BM = \sqrt{AB^2-AM^2} = \sqrt{13^2-5^2} = \sqrt{144} = 12[/m]
Но ΔBDM - тоже прямоугольный, поэтому:
[m]DM = \sqrt{BD^2+BM^2} = \sqrt{9^2+12^2} = \sqrt{225} = 15[/m]
Ответ: 15