Задача 80737 Помогите решить задачи по геометрии...
Условие

Решение
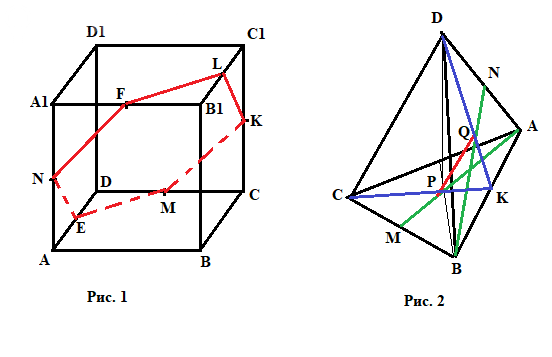
Сечение куба этой плоскостью показано красным.
Это самое трудное сечение куба: 6-угольник EMKLFN.
Все вершины сечения - середины соответствующих стоон.
Заметьте, что сечение проходит через три пары противоположных параллельных граней.
AD (т. E) и B1C1 (т. L); A1B1 (т. F) и CD (т. M); AA1 (т. N) и CC1 (т. K).
5.52. Чертеж к этой задаче смотрите на Рис. 2.
Медианы AM и BN показаны зеленым цветом.
Проведём дополнительно медианы DK и CK.
Как известно, точка пересечения медиан делит их в отношении 1:2.
Очевидно, точки P и Q - это и есть точки пересечения медиан.
Правда, как доказать, что при этом получится PQ || CD - я не знаю.
Но будем считать, что это так и есть. Тогда:
QK = 1/2*DQ = 1/3*DK
PK = 1/2*CP = 1/3*CK
То есть, по теореме Фалеса, в треугольнике DCK будет
[b]PQ = 1/3*CD[/b]
6.2. Это самая простая задача из этих трёх.
Так как ABCD и AEFD - параллелограммы с общей стороной AD,
то |EF| = |AD| = |BC| = a см.
Поэтому плоскость DCF получается из плоскости ABE параллельным переносом на длину a см.
Естественно, что эти плоскости параллельны друг другу.