Задача 80736 Помогите пожалуйста решить задание 9.3...
Условие

Решение
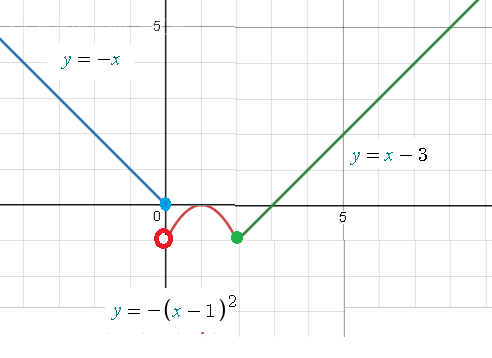
На (0;2) функция непрерывна, так как y=-(x-1)^2 непрерывна на (- ∞ ;+ ∞ )
На (2;+ ∞ ) функция непрерывна, так как y=x-3 непрерывна на (- ∞ ;+ ∞ )
Значит, надо выяснить непрерывность функции в точках
х=0 и х=2
х=0
Находим предел слева:
lim_(x → -0)f(x)=lim_(x → -0)(-x)=-(-0)=0
Находим предел справа:
lim_(x →+0)f(x)=lim_(x → +0)(-(x-1)^2)=-(+0-1)^2=-1
предел слева НЕ равен пределу справа
Значит х=0 - [i]точка разрыва первого рода[/i]
x=2
Находим предел слева:
lim_(x →2 -0)f(x)=lim_(x → 2-0)(-(x-1)^2)=-(2-0-1)^2=-1
Находим предел справа:
lim_(x →2 +0)f(x)=lim_(x → 2+0)(x-3)=2+0-3=-1
х=2 - [i]точка непрерывности [/i]
предел слева = пределу справа и равен значению функции в точке 2
f(2)=2-3=-1
х=3 - [i]точка непрерывности [/i]