Задача 80697 Постройте сечение правильного тетраэдра...

6944459afc938919023f4557

12/18/2025 6:33:52 PM

Постройте сечение правильного тетраэдра ABCD плоскостью,
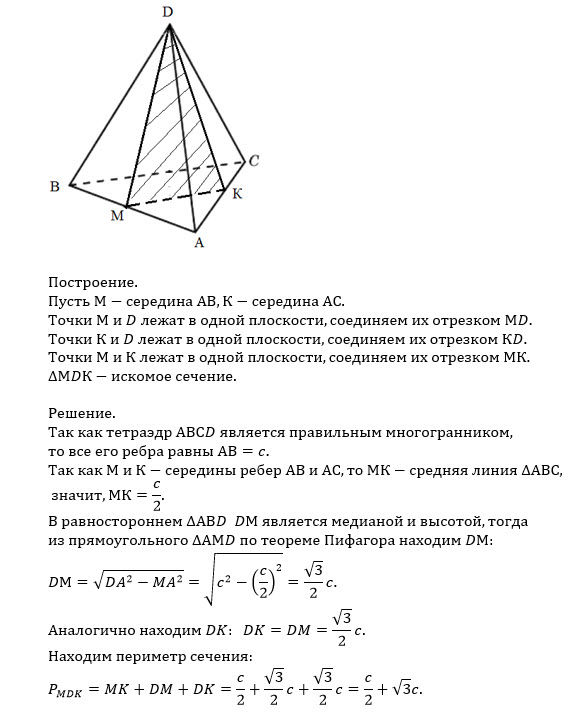
которая проходит через вершину D и середины ребер AB и AC.
Найдите периметр и площадь сечения, если ???????? = ????

5f3ea7e3faf909182968ddd9

12/18/2025 7:33:12 PM

★

MN- средняя линия Δ АВС
MN=c/2
DM=DN-высоты равносторонних треугольников ACD и ADB
DM=DN=csqrt(3)/2

Сечение DMN - равнобедренный треугольник

[b]P_( Δ DMN)[/b]=MN+DM+DN=(c/2)+(csqrt(3)/2)+(csqrt(3)/2=[b](c/2)+csqrt(3)[/b]


Найдем высоту равнобедренного треугольника DMN

DK^2=DM^2-MK^2 ( K - середина MN)

DK^2=(csqrt(3)/2)^2-(c/4)^2=11c^2/16

DK=csqrt(11)/4

S_( Δ MDN)=(1/2)MN*DK=(1/2)*(c/2)*(csqrt(11)/4)=[b]c^2sqrt(11)/16
[/b]

[i] второй способ[/i]
Найдем угол MDN по теореме косинусов

cos ∠ MDN=(DM^2+DN^2-MN^2)/(2*DM*DN)


cos ∠ MDN=[b]([/b](3c^2/4)+(3c^2/4)-(c^2/4)[b])[/b]/[b]([/b]2*(csqrt(3)/2)*(csqrt(3)/2)[b])[/b]


cos ∠ MDN=5/6

sin ∠ MDN=sqrt(1-(5/6)^2)=sqrt(11)/6


S_( Δ MDN)=(1/2)DM*DN*sin ∠ MDN=(1/2)*(csqrt(3)/2)*(csqrt(3)/2)*sqrt(11)/6=[b]c^2*sqrt(11)/16[/b]