Задача 80696 ...
Условие
1.1. ∫ dx / (6 - 2x)
колледж
35
Решение
★
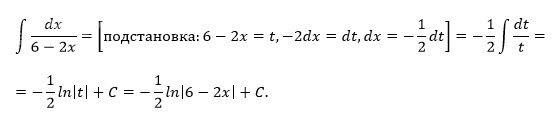
Все решения
Есть табличный интеграл:
[m]\int \frac{dx}{x} = \ln |x| + C[/m]
И есть правило деления на коэффициент:
[m]\int f(ax + b) dx = \frac{1}{a} \cdot F(ax + b) + C[/m]
где F(ax + b) - это первообразная подынтегральной функции.
Применяем это правило на этом интеграле:
[m]\int \frac{dx}{6 - 2x} = \frac{1}{-2} \cdot \ln |6 - 2x| + C = -\frac{1}{2} \cdot \ln |6 - 2x| + C[/m]