Задача 80688 ...
Условие

Решение
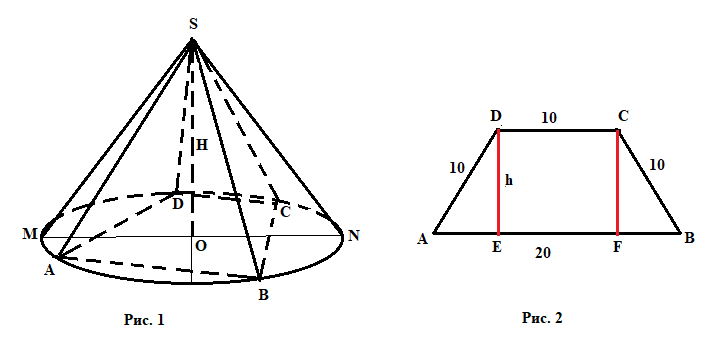
Есть пирамида, у которой в основании равносторонняя трапеция.
Равносторонняя - это значит, что малое основание равно боковым сторонам.
AB = 20 см, BC = CD = AD = 10 см.
На Рис. 2 трапеция нарисована отдельно.
Проводим две высоты, DE и CF, они обозначены красным.
AB = AE + EF + FB
Так как трапеция равнобедренная, то:
EF = CD = 10 см.
AE = FB = (AB - EF)/2 = (20 - 10)/2 = 5 см.
В прямоугольном треугольнике ADE получаем: AD = 10, AE = 5,
DE = h = sqrt(AD^2 - AE^2) = sqrt(10^2 - 5^2) = sqrt(75) = 5sqrt(3) см
Площадь трапеции:
S(ABCD) = (AB + CD)*H/2 = (20 + 10)*5sqrt(3)/2 = 75sqrt(3) см^2
Объем конуса равен:
[m]V(к) = \frac{1}{3} \cdot \pi \cdot R^2 \cdot H[/m] см^3
По условию он равен:
[m]V(кон) = \frac{1000 \pi \sqrt{3}}{3}[/m] см^3
Отсюда:
[m]R^2 \cdot H = 1000 \sqrt{3} = 10^2 \cdot 10 \sqrt{3}[/m]
Значит: R = 10 см, H = 10sqrt(3) см
Объем пирамиды:
[m]V(пир) = \frac{1}{3} S(ABCD) \cdot H = \frac{1}{3} \cdot 75\sqrt{3} \cdot 10\sqrt{3} = 750[/m] см^3
Ответ: 750 см^3