Задача 80687 основанием прямой призмы является ромб с...

694bf6a4928b994c33a23c36

12/24/2025 2:22:22 PM

основанием прямой призмы является ромб с острым углом 60*и стороной, равной 6. Найдите обьем призмы, если ее высота равна длине большей диагонали ромба, лежащего в основании. При выполнении задания необходимо сделать рисунок

692ecb44a0211e4a1fadc32d

12/24/2025 6:04:57 PM

★

Дано: ABCDA1B1C1D1 - прямая призма;
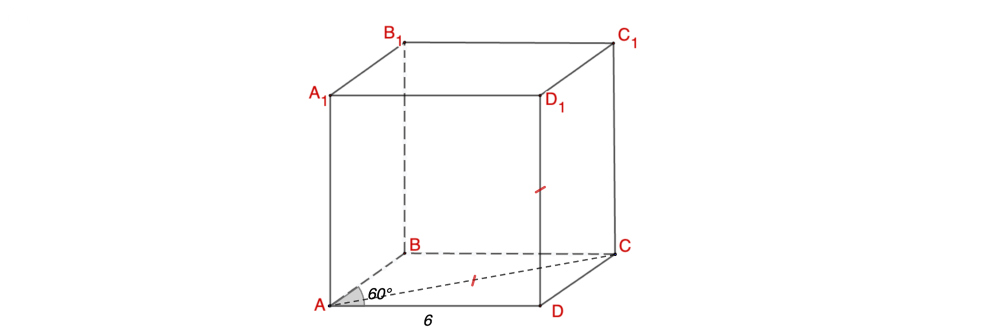
ABCD - ромб; ∠ А = 60 ° ; AB = 6
AC = AA1
Найти: V призмы
Решение:
ABCD - ромб;
∠ А = 60 °
Сумма углов ромба, прилежащих к одной стороне, равна 180 ° .
⇒ ∠ D = 180 ° - 60 ° = 120 °
Из ΔACD по теореме косинусов найдем АС:
[m]AC^2=AD^2+DC^2-2\cdot AD\cdot DC\cdot cos120^0=

\\\\=36 + 36 - 2\cdot6\cdot6\cdot(-\frac{1}{2} ) =108

\\\\AC=6\sqrt{3}[/m]
⇒ [m]AA1=6\sqrt{3}[/m]
Объем призмы равен произведению площади основания на высоту.
[m]\displaystyle S_{OCH.}=AB\cdot AD\cdot sin60^0=36\cdot \frac{\sqrt{3}}{2} =18\sqrt{3} [/m]

[m]\displaystyle V=18\sqrt{3}\cdot 6\sqrt{3}=324[/m] (куб.ед)