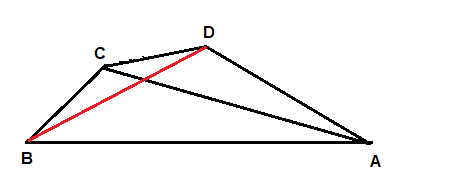
Задача 80657 интересует ответ под б)...
Условие

Решение
б) Найти BD.
Решение:
1) Рассмотрим треугольник ACD. Найдем угол D из теоремы косинусов.
[m]AC^2 = DA^2 + CD^2 - 2 \cdot DA \cdot CD \cdot \cos D[/m]
[m]\frac{45^2}{2} = \frac{45^2}{4} + \frac{45^2(2 - \sqrt{3})}{4} - 2 \cdot \frac{45}{2} \cdot \frac{45 \sqrt{2 - \sqrt{3}}}{2} \cdot \cos D[/m]
Делим левую и правую части на 45^2:
[m]\frac{1}{2} = \frac{1}{4} + \frac{2 - \sqrt{3}}{4} - \frac{\sqrt{2 - \sqrt{3}}}{2} \cdot \cos D[/m]
Выделим cos D:
[m]\frac{\sqrt{2 - \sqrt{3}}}{2} \cdot \cos D = \frac{1}{4} + \frac{2 - \sqrt{3}}{4}- \frac{2}{4}[/m]
[m]\frac{\sqrt{2 - \sqrt{3}}}{2} \cdot \cos D = \frac{1 - \sqrt{3}}{4}[/m]
Заметим, что:
[m]\frac{\sqrt{2 - \sqrt{3}}}{2} = \sqrt{\frac{2 - \sqrt{3}}{4}} = \sqrt{\frac{4 - 2\sqrt{3}}{8}} = \sqrt{\frac{3 - 2\sqrt{3}+1}{8}}= [/m]
[m]= \sqrt{\frac{(\sqrt{3}-1)^2}{8}} = \frac{\sqrt{3}-1}{\sqrt{8}} = \frac{\sqrt{2}(\sqrt{3}-1)}{4}[/m]
Подставляем в формулу cos D:
[m]\cos D = \frac{1 - \sqrt{3}}{4} : \frac{\sqrt{2}(\sqrt{3}-1)}{4} = \frac{1 - \sqrt{3}}{4} \cdot \frac{4}{\sqrt{2}(\sqrt{3}-1)} = -\frac{1}{\sqrt{2}}[/m]
Угол [b]D = 3π/4 = 135°[/b]
[b]sin D = sqrt(2)/2[/b]
2) Точно также рассмотрим треугольник ABC. Найдем угол B.
[m]AC^2 = AB^2 + BC^2 - 2 \cdot AB \cdot BC \cdot \cos B[/m]
[m]\frac{45^2}{2} = \frac{45^2 \cdot 3}{4} + \frac{45^2(2 - \sqrt{3})}{4} - 2 \cdot \frac{45 \cdot \sqrt{3}}{2} \cdot \frac{45 \sqrt{2 - \sqrt{3}}}{2} \cdot \cos B[/m]
Делим левую и правую части на 45^2:
[m]\frac{1}{2} = \frac{3}{4} + \frac{2 - \sqrt{3}}{4} - \frac{\sqrt{3} \cdot \sqrt{2 - \sqrt{3}}}{2} \cdot \cos B[/m]
Выделим cos B:
[m]\frac{\sqrt{3} \cdot \sqrt{2 - \sqrt{3}}}{2} \cdot \cos B = \frac{3}{4} + \frac{2 - \sqrt{3}}{4} - \frac{2}{4}[/m]
[m]\frac{\sqrt{3} \cdot \sqrt{2 - \sqrt{3}}}{2} \cdot \cos B = \frac{3 - \sqrt{3}}{4} = [/m]
Как мы уже знаем:
[m]\frac{\sqrt{2 - \sqrt{3}}}{2} = \frac{\sqrt{2}(\sqrt{3}-1)}{4}[/m]
Поэтому:
[m]\cos B = \frac{3 - \sqrt{3}}{4} : \frac{\sqrt{3} \cdot \sqrt{2}(\sqrt{3}-1)}{4} = \frac{3 - \sqrt{3}}{4} \cdot \frac{4}{\sqrt{2} \cdot (3 - \sqrt{3})} = \frac{1}{\sqrt{2}}[/m]
Угол [b]B = π/4 = 45°[/b]
sin B = sqrt(2)/2
3) Теперь, зная углы B и D, мы можем по теореме синусов найти углы:
Угол ACD из треугольника ACD.
[m]\frac{AC}{\sin ADC} = \frac{DA}{\sin ACD}[/m]
[m]\frac{45}{\sqrt{2}} : \frac{\sqrt{2}}{2} = \frac{45}{2} : \sin ACD[/m]
[m]\sin ACD = \frac{45}{2} \cdot \frac{\sqrt{2}}{2} : \frac{45}{\sqrt{2}} = \frac{\sqrt{2}\sqrt{2}}{4} = \frac{1}{2}[/m]
[b]ACD = π/6 = 30°[/b]
Угол ACB из треугольника ABC:
[m]\frac{AC}{\sin ABC} = \frac{AB}{\sin ACB}[/m]
[m]\frac{45}{\sqrt{2}} : \frac{\sqrt{2}}{2} = \frac{45 \sqrt{3}}{2} : \sin ACB[/m]
[m]\sin ACB = \frac{45\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2} : \frac{45}{\sqrt{2}} = \frac{\sqrt{3}\sqrt{2}\sqrt{2}}{4} = \frac{\sqrt{3}}{2}[/m]
[b]ACB = π/3 = 60°[/b]
Таким образом, мы получили, что угол BCD:
BCD = ACD + ACB = 30° + 60° = 90°
То есть треугольник BCD - прямоугольный.
BD вычисляем по теореме Пифагора:
[m]BD = \sqrt{BC^2 + CD^2} = \sqrt{\frac{45^2 (2 - \sqrt{3})}{4} + \frac{45^2 (2 - \sqrt{3})}{4}} = [/m]
[m]= \sqrt{\frac{45^2 (2 - \sqrt{3})}{4} \cdot 2} = 45\sqrt{2} \frac{\sqrt{2 - \sqrt{3}}}{2} =45\sqrt{2}\frac{\sqrt{2}(\sqrt{3}-1)}{4} = \frac{45(\sqrt{3}-1)}{2}[/m]
На чертеже я нарисовал, как смог. Угол B = 45 °, D = 135 °.
Правда, угол C не получился равным 90°.