Задача 80656 Наити max min...
Условие
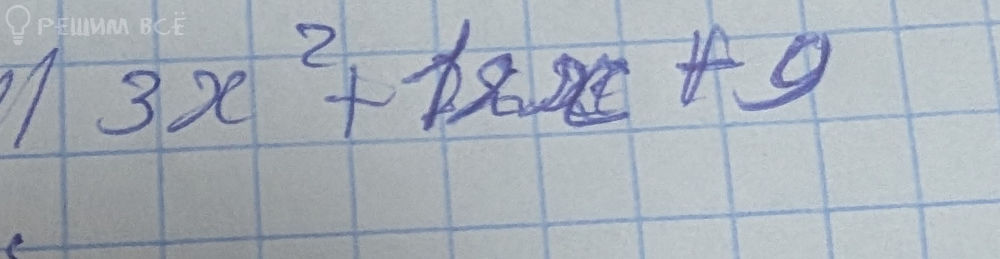
математика 10-11 класс
17
Решение
★
y = 3x^2 + 12x + 9
Если коэффициенты другие, то подставьте свои.
К счастью ясно, что это парабола, и она имеет 1 экстремум.
Рассмотрим коэффициент при x^2, он равен 3.
3 > 0, значит, ветви параболы направлены вверх.
Вершина - это точка минимума, найдем ее.
x0 = -b/(2a) = -12/(2*3) = -12/6 = -2
y0 = y(x0) = y(-2) = 3(-2)^2 + 12(-2) + 9 = 12 - 24 + 9 = -3
Если надо найти через производную, то вот второе решение.
В точке экстремума производная равна 0.
y' = 3*2x + 12 = 0
6x + 12 = 0
6x = -12
x0 = -2, y0 = y(-2) = -3
Результат точно такой же.
Ответ: Точка минимума - M0(-2; -3)