Задача 80653 Решите пожалуйста...
Условие
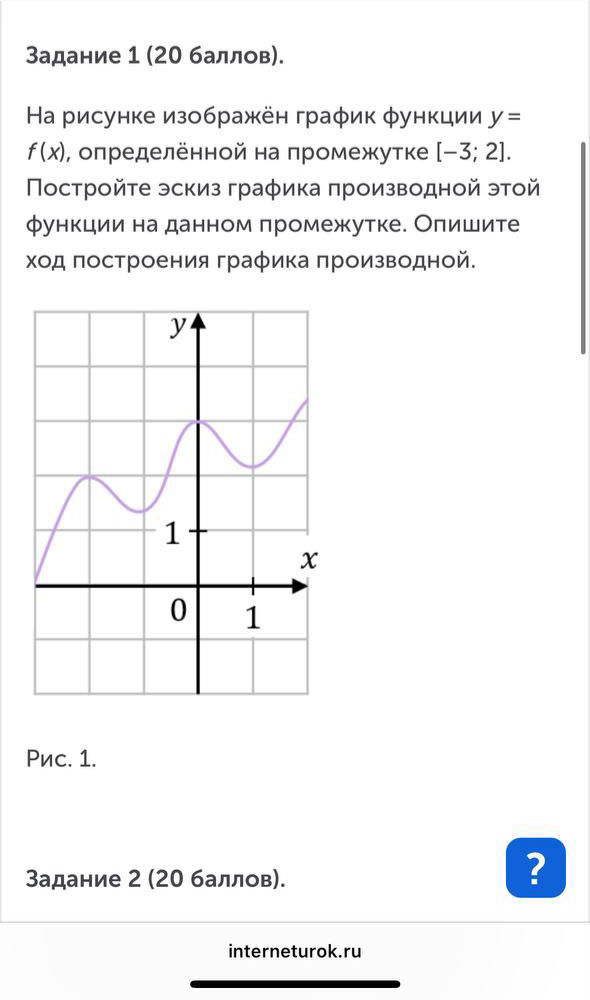


Решение
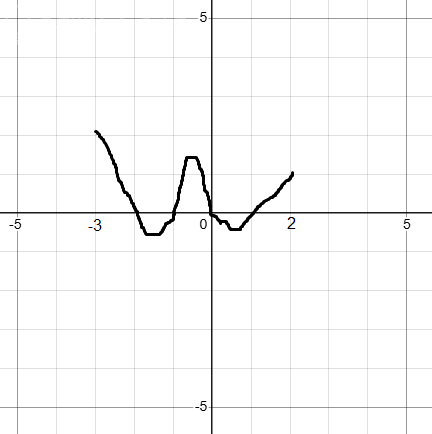
Там, где функция возрастает - производная положительна.
Там, где функция убывает - производная отрицательна.
В точках экстремумов производная равна 0.
Примерный график смотрите на рисунке 1.
2) Прибыль: [m]P(x) = \frac{8x}{x^2+4}[/m], где x - это цена товара.
Прибыль будет максимальной в точке, где производная равна 0.
[m]P'(x) = \frac{8(x^2 + 4) - 8x \cdot 2x}{(x^2 + 4)^2} = \frac{8x^2 + 32 - 16x^2}{(x^2 + 4)^2} = \frac{32 - 8x^2}{(x^2 + 4)^2} = 0[/m]
32 - 8x^2 = 0
8x^2 = 32
x^2 = 4
x = 2, потому что цена должна быть положительной.
Прибыль при этом:
[m]P(2) = \frac{8 \cdot 2}{2^2+4} = \frac{16}{4+4} = 2[/m]
Ответ: P(2) = 2
3) f(x) = x^3 + 3x, x0 = 3
а) Уравнение касательной:
y(x) = f(x0) + f'(x0)*(x - x0)
f(x0) = f(3) = 3^3 + 3*3 = 27 + 9 = 36
f'(x) = 3x^2 + 3
f'(x0) = f'(3) = 3*3^2 + 3 = 27 + 3 = 30
Уравнение касательной:
y(x) = 36 + 30*(x - 3)
y(x) = 36 + 30x - 90
Ответ: y(x) = 30x - 54
б) Другая касательная, параллельная данной, должна иметь такой же коэффициент k = 30.
f'(x) = 3x^2 + 3 = 30
3x^2 = 27
x^2 = 9
x1 = -3, x2 = 3
Вторая точка: x = -3, f(-3) = (-3)^3 + 3(-3) = -27 - 9 = -36
Ответ: B(-3; -36)
4) f(x) = -x^2 + 6x; g(x) = 0
Находим точки пересечения, это будут границы интегрирования.
-x^2 + 6x = 0
x(-x + 6) = 0
x1 = 0, x2 = 6
Площадь под графиком:
[m]S = \int \limits_0^6 (-x^2 + 6x) dx = -\frac{x^3}{3} + \frac{6x^2}{2} \bigg |_0^6 =[/m]
[m]= -\frac{6^3}{3} + 3 \cdot 6^2 - (-0 + 0) = -72 + 108 = 36[/m]
Ответ: S = 36
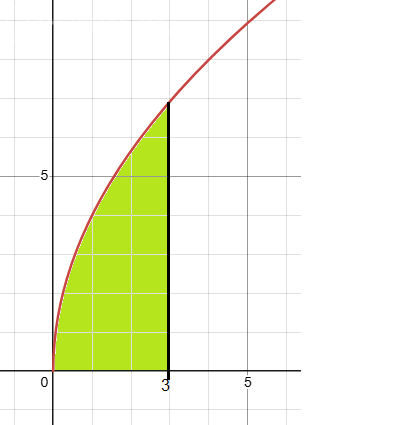
5) [m]y = 4 \sqrt{x}[/m]; x = 3; y = 0
Эта фигура показана на рисунке 2, закрашена зеленым.
Нам надо найти объем теле, образованного этой фигурой при вращении вокруг оси Ox.
Для этого есть специальная формула:
[m]V = π \int \limits_0^3 f^2(x) dx = π \int \limits_0^3 16x dx = π \cdot 8x^2 \bigg |_0^3 =[/m]
[m]= π (8 \cdot 3^2 - 8 \cdot 0) = π \cdot 8 \cdot 9 = 72π[/m]
Ответ: V = 72π