Задача 80652 ...
Условие
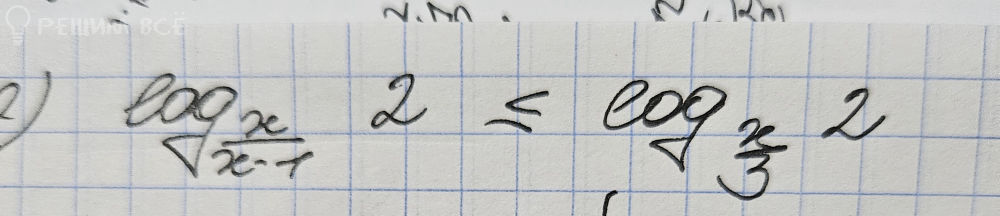
Решение

Все решения
log_{√(x ⁄ (2x – 7))} 2 ≤ log_{√3} 2. (1)
1. Область допустимых значений
• Основание логарифма должно быть положительным и ≠1:
√(x ⁄ (2x – 7)) > 0, √(x ⁄ (2x – 7)) ≠ 1.
• Доля x ⁄ (2x – 7) должна быть положительной:
x/(2x – 7) > 0.
Знаки числителя и знаменателя совпадают:
x = 0, 2x – 7 = 0 → x = 7⁄2.
x < 0 ⇒ x/(2x – 7) > 0
0 < x < 7⁄2 ⇒ x/(2x – 7) < 0 (нет)
x > 7⁄2 ⇒ x/(2x – 7) > 0.
Значит
x ∈ (−∞,0) ∪ (7⁄2, +∞).
Условие «основание ≠1»:
x/(2x – 7) ≠ 1 ⇒ x = 7 (исключается).
2. Сравнение логарифмов
Запишем оба логарифма через натуральный:
log_{a} 2 = ln 2 / ln a, где a = √(x/(2x – 7)).
Неравенство (1) эквивалентно
1/ln a ≤ 1/ln√3, (2)
потому что ln 2 > 0.
Рассматриваем два случая, зависящих от знака ln a (т.е. от того, больше или меньше a единицы).
• Случай a < 1 (ln a < 0).
Левая часть (2) — отрицательна, правая — положительна, значит
неравенство выполняется автоматически.
Условие a < 1 ↔ x/(2x – 7) < 1.
x/(2x – 7) < 1
⇒ (x − (2x – 7))/(2x – 7) < 0
⇒ (7 − x)/(2x – 7) < 0.
Точки 3.5 и 7 делят числовую прямую на интервалы
(−∞,3.5), (3.5,7), (7,+∞).
Знак выражения (7 – x)/(2x – 7):
x < 3.5 : (+)/(−) → «−» (<0) ✔
3.5 < x < 7 : (+)/(+) → «+» (>0) ✖
x > 7 : (−)/(+) → «−» (<0) ✔
С учётом ОДЗ получаем
a < 1 ⇔ x ∈ (−∞,0) ∪ (7,+∞).
• Случай a > 1 (ln a > 0).
Тогда (2) эквивалентно ln a ≥ ln√3 ⇔ a ≥ √3.
a = √(x/(2x – 7)) ≥ √3
⇒ x/(2x – 7) ≥ 3.
Находим, где x/(2x – 7) > 1 (чтобы a > 1).
Это тот же промежуток (3.5, 7). Решаем там неравенство:
x ≥ 3(2x – 7)
⇒ x ≥ 6x − 21
⇒ 5x ≤ 21
⇒ x ≤ 21/5 = 4.2.
Итак,
3.5 < x ≤ 4.2 ⇒ x ∈ (7⁄2, 21⁄5].
3. Итоговое множество решений (объединяем два полученных набора):
x ∈ (−∞,0) ∪ (7⁄2, 21⁄5] ∪ (7,+∞).
4. Точка x = 7 исключается (основание логарифма равно 1).
Ответ:
(−∞,0) ∪ (7⁄2, 21⁄5] ∪ (7,+∞).