Задача 80651 4.2.96. Найти площадь треугольника,...
Условие
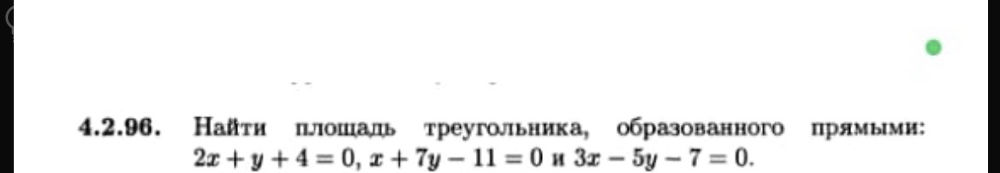
Решение
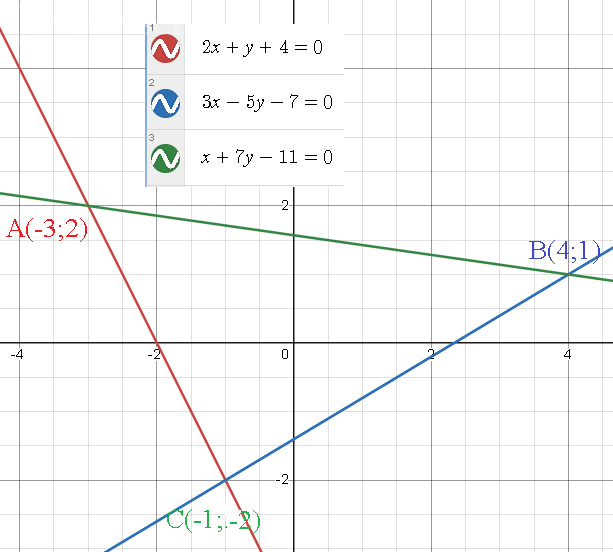
Нужно найти точки пересечения этих прямых, для этого нужно решить системы уравнений:
{ 2x + y + 4 = 0
{ x + 7y - 11 = 0
Умножаем 2 уравнение на -2:
{ 2x + y + 4 = 0
{ -2x - 14y + 22 = 0
Складываем уравнения:
-13y + 26 = 0
13y = 26, y = 2
Подставляем в любое уравнение:
2x + 2 + 4 = 0
2x = -6; x = -3
[b]A(-3; 2)[/b]
{ 2x + y + 4 = 0
{ 3x - 5y - 7 = 0
Умножаем 1 уравнение на 5:
{ 10x + 5y + 20 = 0
{ 3x - 5y - 7 = 0
Складываем уравнения:
13x + 13 = 0; x = -1
Подставляем в любое уравнение:
3(-1) - 5y - 7 = 0
-5y = 10; y = -2
[b]B(-1; -2)[/b]
{ x + 7y - 11 = 0
{ 3x - 5y - 7 = 0
Умножаем 1 уравнение на -3:
{ -3x - 21y + 33 = 0
{ 3x - 5y - 7 = 0
Складываем уравнения:
-26y + 26 = 0; y = 1
Подставляем в любое уравнение:
x + 7*1 - 11 = 0
x + 7 - 11 = 0; x = 4
[b]C(4; 1)[/b]
Находим длину стороны треугольника AB:
a = |AB| = sqrt((-1+3)^2 + (-2-2)^2) = sqrt(2^2 + (-4)^2) = sqrt(20) = 2sqrt(5)
[b]a = 2sqrt(5)[/b]
Находим расстояние от точки C(4; 1) до прямой AB: 2x + y + 4 = 0
Расстояние от точки M(x0; y0) до прямой Ax + By + C = 0:
[m]\large h = \frac{|A \cdot x0 + B \cdot y0 + C|}{\sqrt{A^2+B^2}}[/m]
Подставляем:
[m]\large h = \frac{|2 \cdot 4 + 1 \cdot 1 + 4|}{\sqrt{2^2+1^2}} = \frac{|8 + 1 + 4|}{\sqrt{4+1}} = \frac{13}{\sqrt{5}}[/m]
Это расстояние является высотой треугольника, опущенной на AB.
Площадь треугольника находим по формуле:
[m]\large S(Δ) = \frac{1}{2} \cdot a \cdot h = \frac{1}{2} \cdot 2 \sqrt{5} \cdot \frac{13}{\sqrt{5}} = \frac{2 \sqrt{5} \cdot 13}{2 \cdot \sqrt{5}} = 13[/m]
[b]Ответ: S(Δ) = 13[/b]
Все решения
2x+y+4=0 ⇒ y = –2x – 4
x+7y-11=0 ⇒ y = (11 – x)/7
Приравниваем правые части
–2x – 4 = (11 – x)/7 ⇒ –14x – 28 = 11 – x ⇒ –13x = 39 ⇒ x = –3
y = –2(–3) – 4 = 2.
A(–3, 2).
3x-5y-7=0 ⇒ y= (3x – 7)/5
x+7y-11=0 ⇒ y=(11 – x)/7
Приравниваем правые части
(3x – 7)/5 =(11 – x)/7 ⇒ 5(11 – x) = 7(3x – 7) ⇒ 55 – 5x = 21x – 49 ⇒ 104 = 26x ⇒ x = 4
y = (11 – 4)/7 = 1.
B(4, 1).
2x+y+4=0 ⇒ y = –2x – 4
3x-5y-7=0 ⇒ y= (3x – 7)/5
Приравниваем правые части
–2x – 4 = (3x – 7)/5 ⇒ –10x – 20 = 3x – 7 ⇒ –13x = 13 ⇒ x = –1
y = –2(–1) – 4 = –2.
C(–1, –2).
Находим площадь треугольника по координатам его точек
A(-3;2); B(4;1): C(-1;-2)
см. формулу в приложении 2
S=(1/2)*|((-3)*(1-(-2))+4*(-2-2)+(-1)*(2-1))|
S=(1/2)|(-9-16-1)|
S=(1/2)*26
S=13