Задача 80650 Помогите решить 7.3.30...
Условие
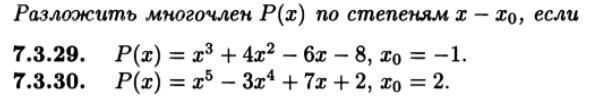
Решение
Первым членом, очевидно, будет (x - 2)^5. Разложим скобку:
(x - 2)^5 = x^5 - 5x^4*2 + 10x^3*2^2 - 10x^2*2^3 + 5x*2^4 - 2^5
(x - 2)^5 = x^5 - 10x^4 + 40x^3 - 80x^2 + 80x - 32
Смотрим на 4 степень. Получилось -10x^4, а нам надо -3x^4.
Значит, прибавляем 7x^4. И меняем знаки у остальных членов:
P(x) = (x - 2)^5 + 7x^4 - 40x^3 + 80x^2 - 80x + 32 + 7x + 2
P(x) = (x - 2)^5 + 7x^4 - 40x^3 + 80x^2 - 73x + 34
Вторым членом будет 7(x - 2)^4.
7(x - 2)^4 = 7(x^4 - 4x^3*2 + 6x^2*2^2 - 4x*2^3 + 2^4)
7(x - 2)^4 = 7x^4 - 56x^3 + 168x^2 - 224x + 112
Смотрим на 3 степень. Получилось -56x^3, а надо -40x^3.
Значит, прибавляем 16x^3. Также смотрим остальные члены:
P(x) = (x - 2)^5 + 7(x - 2)^4 + 16x^3 - 88x^2 + 151x - 78
Третьим членом будет 16(x - 2)^3.
16(x-2)^3 = 16(x^3 - 3x^2*2 + 3x*2^2 - 2^3) = 16x^3 - 96x^2 + 192x - 128
Смотрим x^2: из -96 делаем -88. Смотрим x: из 192 делаем 151.
Смотрим свободный член: из -128 делаем -78.
P(x) = (x - 2)^5 + 7(x - 2)^4 + 16(x - 2)^3 + 8x^2 - 41x + 50
Следующим членом будет 8(x - 2)^2.
8(x - 2)^2 = 8(x^2 - 4x + 4) = 8x^2 - 32x + 32
Последний шаг. Из -32x делаем -41x. И из +32 делаем +50.
P(x) = (x - 2)^5 + 7(x - 2)^4 + 16(x - 2)^3 + 8(x - 2)^2 - 9x + 18
Очередной член -9(x - 2) = -9x + 18. Окончание такое и есть.
P(x) = (x - 2)^5 + 7(x - 2)^4 + 16(x - 2)^3 + 8(x - 2)^2 - 9(x - 2)
Это ответ.
Все решения
P(x) = (x – 2)^5 + 7(x – 2)^4 + 16(x – 2)^3 + 8(x – 2)^2 – 9(x – 2)
Р е ш е н и е
Дифференцируем многочлен 5 раз
P`(x)=(x^5 – 3x^4 + 7x + 2)`=5x^4-12x^3+7
P``(x)=(5x^4-12x^3+7)`=20x^3-36x^2
P```(x)=(20x^3-36x^2)`=60x^2-72x
P^(IV)(x)=(60x^2-72x)`=120x-72
P^(V)(x)=(120x-72)`=120
Находим значения производных в точке x_(о) = 2
P`(2)=5*2^4-12*2^3+7=-9
P``(2)=20*2^3-36*2^2=16
P```(2)=60*2^2-72*2=96
P^(IV)(2)=120*2-72=168
P^(V)(2)=120
Подставляем в формулу
P(x)=[m]\frac{120}{5!}(x-2)^5+\frac{168}{4!}(x-2)^4+\frac{96}{3!}(x-2)^3+\frac{16}{2!}(x-2)^2+\frac{(-9)}{1!}(x-2)^1[/m]
P(x) = (x – 2)^5 + 7(x – 2)^4 + 16(x – 2)^3 + 8(x – 2)^2 – 9(x – 2)