Задача 80649 Написать уравнение касательной и нормали...
Условие
кривой в точке с абсциссой x0: y=2*e^(3-x^2), x0=1.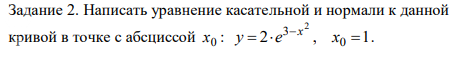
математика ВУЗ
44
Решение
★
y`=2e^(3-x^2)*(-2x)
y`=-4x*e^(3-x^2)
y`(1)=-4*1e^(3-1)
y`(1)=-4e^2
y(1)=2*e^(3-1)
y(1)=2e^2
y-2e^2=-4e^2*(x-1)
[b]y=-4xe^2+6e^2[/b] - уравнение касательной
y-2e^2=(-1.(-4e^2))*(x-1)
y-2e^2=(x-1)/4e^2 - уравнение нормали