Задача 80646 1. Решите уравнение sin 2x = 2cos...
Условие
[5]
2. Решите уравнение с помощью универсальной тригонометрической подстановки: 2sin x + cos x = 1
[2]
3. Решите неравенство 3sin(2x - pi/4) <= 1
[3]
4. Найдите область определения функции y = 3 + sqrt(4tan(x/2) - 5)
5. В корзине лежат 12 яблок, из которых желтых. Наугад выбирают 3 яблока. Какова вероятность того, что среди них окажется ровно 2 зеленых?
[3]
6. а) Запишите три первых члена в разложении (1 - x) ^ 5
[2]
b) Используя разложение, полученное в пункте а, вычислите (0, 98) ^ 5 с точностью до тысячных. Калькулятор применять только на последнем этапе вычислений.
[2]
7. У фирмы - производителя телевизоров три завода: А, В и С. Они производят определенную модель цветных телевизоров с вероятностями 30%, 40% и 30% соответственно. Цветные телевизоры, произведённые на заводе А, составляют 35% всех цветных телевизоров, 45% цветных телевизоров, произведены на заводе В, 20% цветных телевизоров произведены на заводе С.
а) Наугад выбран телевизор, произведенный этой фирмой. Найдите вероятность того, что этот телевизор цветной.
[2]
b) Учитывая, что случайно выбранный телевизор цветной, найти вероятность того, что он произведен на заводе С.
Решение
2sin x*cos x - 2cos x = 0
2cos x*(sin x - 1) = 0
Если произведение равно 0, то один из множителей равен 0.
cos x = 0; x1 = π/2 + π*k, k ∈ Z
sin x = 1; x2 = π/2 + 2π*n, n ∈ Z
Все x2 уже есть в x1, общий ответ: [b]x = π/2 + π*k, k ∈ Z[/b]
2) 2sin x + cos x = 1
Универсальная тригонометрическая подстановка:
[m]\large tg\ \frac{x}{2} = t, \sin x = \frac{2t}{1 + t^2}, \cos t = \frac{1 - t^2}{1 + t^2}[/m]
Подставляем:
[m]\large \frac{4t}{1 + t^2} + \frac{1 - t^2}{1 + t^2} = 1[/m]
Умножаем всё на (1 + t^2):
4t + 1 - t^2 = 1 + t^2
Переносим все направо, чтобы t^2 было с плюсом:
0 = 2t^2 - 4t
Записываем в стандартном виде и раскладываем на скобки:
2t*(t - 2) = 0
а) t1 = 0; tg x/2 = 0; x/2 = π*k;
[b]x1 = 2π*k, k ∈ Z[/b]
б) t2 = 2, tg x/2 = 2, x/2 = arctg 2 + π*n;
[b]x2 = 2*arctg 2 + 2π*n, n ∈ Z[/b]
3) 3sin (2x - π/4) ≤ 1
sin (2x - π/4) ≤ 1/3
Замена 2x - π/4 = t
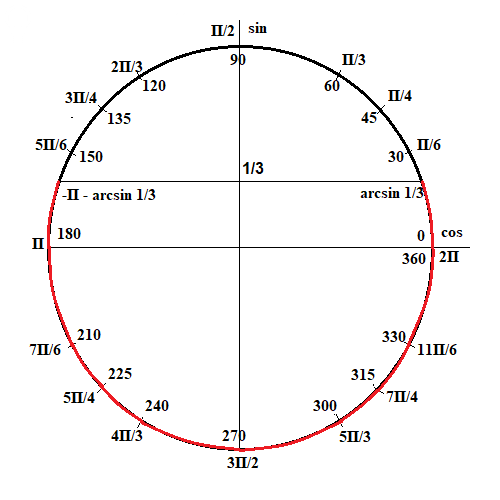
sin t ≤ 1/3
Решение этого неравенства показано на рисунке красным.
Движение идет против часовой стрелки, поэтому начинаем с отрицательного числа -π - arcsin 1/3 + 2π*k, k ∈ Z
и заканчиваем положительным числом arcsin 1/3 + 2π*k, k ∈ Z.
t ∈ [-π - arcsin 1/3 + 2π*k; arcsin 1/3 + 2π*k], k ∈ Z
Обратная замена:
2x - π/4 ∈ [-π - arcsin 1/3 + 2π*k; arcsin 1/3 + 2π*k], k ∈ Z
2x ∈ [-π + π/4 - arcsin 1/3 + 2π*k; π/4 + arcsin 1/3 + 2π*k], k ∈ Z
2x ∈ [-3π/4 - arcsin 1/3 + 2π*k; π/4 + arcsin 1/3 + 2π*k], k ∈ Z
[b]x ∈ [-3π/8 - 1/2*arcsin 1/3 + π*k; π/8 + 1/2*arcsin 1/3 + π*k], k ∈ Z[/b]
4) [m]y = 3 + \sqrt{4tg\ \frac{x}{2} - 5}[/m]
Область определения функции.
Выражение под корнем должно быть неотрицательным.
4 tg x/2 - 5 ≥ 0
tg x/2 ≥ 5/4
x/2 ∈ [arctg 5/4 + π*k; π/2 + π*k), k ∈ Z
[b]x ∈ [2arctg 5/4 + 2π*k; π + 2π*k), k ∈ Z[/b]
5) В корзине 12 яблок, 5 зеленых и 7 желтых. Вынимают 3 яблока.
Нужно получить ровно 2 зеленых яблока.
3 яблока можно вынуть разными способами, нам подходит три:
ЗЗЖ, ЗЖЗ, ЖЗЗ. Рассмотрим каждый способ отдельно.
а) Вероятность достать 1 зеленое яблоко p1 = 5/12.
Остается 11 яблок, из них 4 зеленых.
Вероятность достать 2 зеленое яблоко p2 = 4/11.
Остается 10 яблок, из них 3 зеленых и 7 желтых.
Вероятность достать 3 желтое яблоко p3 = 7/10.
Общая вероятность такого варианта:
P(1) = p1*p2*p3 = 5/12*4/11*7/10 = 5/10*4/12*7/11 = 7/66
б) Вероятность достать 1 зеленое яблоко p1 = 5/12.
Остается 11 яблок, из них 4 зеленых и 7 желтых.
Вероятность достать 2 желтое яблоко p2 = 7/11.
Остается 10 яблок, из них 4 зеленых и 6 желтых.
Вероятность достать 3 зеленое яблоко p3 = 4/10.
Общая вероятность такого варианта:
P(2) = p1*p2*p3 = 5/12*7/11*4/10 = 5/10*4/12*7/11 = 7/66
в) Вероятность достать 1 желтое яблоко p1 = 7/12.
Остается 11 яблок, из них 5 зеленых.
Вероятность достать 2 зеленое яблоко p2 = 5/11.
Остается 10 яблок, из них 4 зеленых.
Вероятность достать 3 зеленое яблоко p3 = 4/10.
Общая вероятность такого варианта:
P(3) = p1*p2*p3 = 7/12*5/11*4/10 = 5/10*4/12*7/11 = 7/66
Итоговая вероятность равна сумме этих вероятностей:
P = P(1) + P(2) + P(3) = 7/66 + 7/66 + 7/66 = 3*7/66 = 7/22
[b]P = 7/22[/b]
6) а) (1 - x)^5 = 1^5 - 5*1^4*x + 10*1^3*x^2 = 1 - 5x + 10x^2
б) (0,98)^5 = (1 - 0,02)^5 = 1 - 5*0,02 + 10*0.02^2 = 1 - 0,1 + 0,004 = 0,904
Калькулятор показывает 0,90392, так что ответ правильный.
7) Предположим, что у нас есть n телевизоров этой фирмы.
Из них 0,35n сделано на заводе A, 0,45n на заводе B и 0,2n на заводе C.
Из 0,35n телевизоров с завода A, ровно 30%, то есть 0,105n - цветные.
Из 0,45n телевизоров с завода B, ровно 40%, то есть 0,18n - цветные.
Из 0,2n телевизоров с завода C, ровно 30%, то есть 0,06n - цветные.
Таким образом, из n телевизоров цветных будет:
0,105n + 0,18n + 0,06n = 0,345n
а) Вероятность, что случайно взятый телевизор - цветной:
[b]P = 0,345n/n = 0,345[/b]
б) Вероятность, что цветной телевизор сделан на заводе C:
[b]P = (0,06n) / (0,345n) = 60/345 = 4/23[/b]