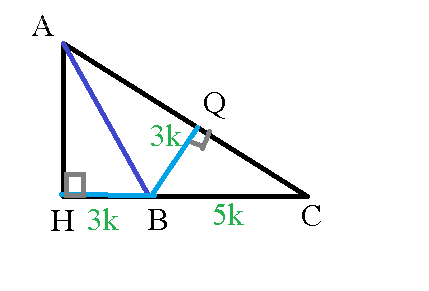
Задача 80635 Из вершин А и В тупоугольного...

693acf9ca0211e4a1fadd0ab

12/11/2025 2:12:20 PM

Из вершин А и В тупоугольного треугольника АВС проведены высоты ВQ и АН. Известно, что угол В - тупой, BH: HC =3:8,BH = BQ.
а) Докажите, что диаметр описанной вокруг треугольника АВО окружности в 5 раз больше BQ.
б) Найдите площадь ВОС, если площадь АНС равна 32.

5f3ea7e3faf909182968ddd9

12/15/2025 9:15:59 PM

★

Δ ABH= Δ ABQ ( по гипотенузе АВ и катету НB=BQ) ⇒ AH=AQ=t

НВ:НС=3:8
НВ=3k
HC=8k
BC=8k-3k=5k

По теореме Пифагора из Δ ВQC
QC=4k


По теореме Пифагора из Δ AHC

AH^2+HC^2=AC^2
t^2+(8k)^2=(t+4k)^2

t^2+64k^2=t^2+8kt+16k^2

t=6k

АН=6k
AC=10k
HC=8k



a) Доказать, что диаметр в пять раз больше BQ=3k
значит этот диаметр должен быть равен 15k

Если речь идет о треугольнике АВQ
Он прямоугольный. Его диаметр это АВ
АВ^2=BQ^2+AQ^2
AB^2=(3k)^2+(6k)^2
AB^2=45k^2
AB=3sqrt(5)*k

AB больше BQ [b]в sqrt(5)[/b] раз


б) S_( Δ AHC)=(1/2)*HC*AH
S_( Δ AHC)=(1/2)*8k*6k
24k^2=32

k^2=32/24

k^2=4/3

S_( Δ ABQ)=(1/2)*BQ*AQ=(1/2)*(3k)*(6k)=9k^2=9*(4/3)=[b]12[/b]