Задача 8062 Угол АСО равен 34°, где О — центр...

echan2018

23.03.2016

Угол АСО равен 34°, где О — центр окружности. Его сторона СА касается окружности. Сторона СО пересекает окружность в точке В (см. рис.). Найдите величину меньшей дуги АВ окружности. Ответ дайте в градусах.

Найдем сначала угол AOC, так как этот угол опирается на дугу AB. По правилу центральный угол равен радианной/градусной мере дуги, на которую опирается.
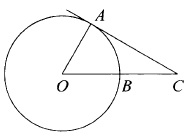
Треугольник является прямоугольным, так как АС касательная, а угол между касательной и радиусом проведённым к точке касания равен 90º.
По свойству прямоугольного треугольника сумма его острых углов равна 90º, значит:
34+∠ACO=90
∠ACO=90-34=56 ⇒ Дуга AB=56


Ответ: 56