Задача 80614 1. Даны координаты точек A(-6; -8), B(2...

69345882a0211e4a1fadc981

12/6/2025 4:23:56 PM

1. Даны координаты точек A(-6; -8), B(2 корень из 6 ; 4) и радиус окружности R=10, центр которой находится в начале координат. Требуется составить каноническое уравнение гиперболы, проходящей через данные точки A и B, если фокусы гиперболы расположены на оси абсцисс;
2. найти полуоси, фокусы, эксцентриситет и уравнения асимптот этой гиперболы;
3. построить гиперболу, ее асимптоты и окружность

626fab9a354ab65fb2f43abb

12/7/2025 6:47:19 PM

★

С окружностью всё ясно, её каноническое уравнение:
x^2 + y^2 = 100
Каноническое уравнение гиперболы:
[m]\large \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1[/m]
Подставляем наши точки A(-6; -8); B(2sqrt(6); 4). Получаем систему:
[m]\large \begin{cases}
\frac{36}{a^2} - \frac{64}{b^2} = 1 \\
\frac{24}{a^2} - \frac{16}{b^2} = 1 \\
\end{cases}[/m]
Избавляемся от дробей:
[m] \begin{cases}
36b^2 - 64a^2 = a^2b^2 \\
24b^2 - 16a^2 = a^2b^2 \\
\end{cases}[/m]
Приравниваем левые части, которые равны a^2b^2:
[m]36b^2 - 64a^2 = 24b^2 - 16a^2[/m]
[m]12b^2 = 48a^2[/m]
[m]b^2 = 4a^2[/m]
Подставляем в любое уравнение:
[m]36 \cdot 4a^2 - 64a^2 = a^2 \cdot 4a^2[/m]
[m]80a^2 = 4a^4[/m]
[m]a^2 = 20[/m]
[m]b^2 = 4a^2 = 80[/m]
Получаем уравнение гиперболы:
[m]\large \frac{x^2}{20} - \frac{y^2}{80} = 1[/m]
Полуоси гиперболы:
[m]a = \sqrt{20} = 2\sqrt{5}; \ b = \sqrt{80} = 4\sqrt{5}[/m]
Фокусы:
[m]c = \sqrt{a^2+b^2} = \sqrt{20+80} = \sqrt{100} = 10[/m]
[m]F_1(-c; 0) = (-10; 0);\ F_2(c; 0) = (10; 0)[/m]
Эксцентриситет:
[m]\large ε = \frac{c}{a} = \frac{10}{2\sqrt{5}} = \sqrt{5}[/m]
Директрисы:
[m]\large x1 = -\frac{a}{ε} = -\frac{2\sqrt{5}}{\sqrt{5}} = -2;\ x2 = \frac{a}{ε} = \frac{2\sqrt{5}}{\sqrt{5}} = 2[/m]
Асимптоты:
[m]\large y1 = -\frac{b}{a} \cdot x = -\frac{4\sqrt{5}}{2\sqrt{5}} \cdot x = -2x[/m]
[m]\large y2 = \frac{b}{a} \cdot x = \frac{4\sqrt{5}}{2\sqrt{5}} \cdot x = 2x[/m]
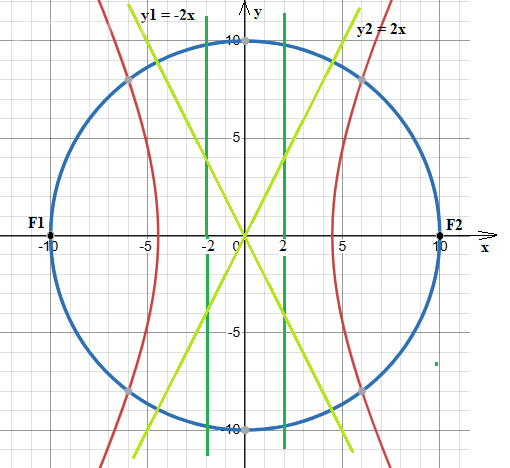
Обе фигуры - окружность и гипербола - представлены на рисунке.
Директрисы (зеленые) и асимптоты (салатовые) гиперболы
также представлены на рисунке.