Задача 80606 2. Через вершину А прямоугольника ABCD...
Условие
Решение
К ∉ (АВС)
КА ⊥ (АВС); КА = 6; КВ = 7; КС = 9.
Найти: КА
Решение:
КА ⊥ (АВС) ⇒ АВ - проекция КВ на (АВС)
АВ ⊥ ВС ⇒ КВ ⊥ ВС (теорема о трех перпендикулярах)
По теореме Пифагора для Δ ВКС:
KB^2 = KC^2-KB^2= 81 - 49 = 32
Противоположные стороны прямоугольника равны.
⇒ BC^2 = AD^2 = 32
По теореме Пифагора для Δ AKD:
AD^2 = KD^2 - AD^2 = 36 - 32 = 4 ⇒ [b]AK = 2[/b]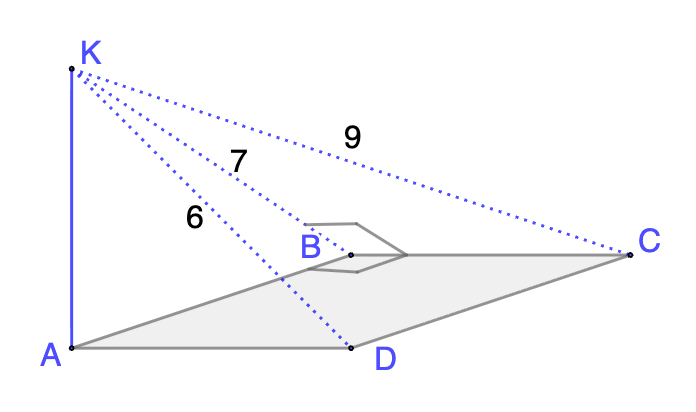
Все решения
• ABCD – прямоугольник,
• AK ⟂ (ABCD),
• h = AK – искомое расстояние от точки K до плоскости ABCD.
Обозначим a = AB, d = AD.
Тогда, по теореме Пифагора, для трёх прямоугольных треугольников с общей высотой h имеем
KD² = d² + h², (1)
KB² = a² + h², (2)
KC² = a² + d² + h², (3) (потому что AC² = a² + d²).
Подставим известные длины KD = 6, KB = 7, KC = 9:
d² + h² = 36, (1′)
a² + h² = 49, (2′)
a² + d² + h² = 81. (3′)
Из (1′) и (2′): d² = 36 – h², a² = 49 – h².
Сложим эти два равенства и прибавим h²:
a² + d² + h² = (49 – h²) + (36 – h²) + h² = 85 – h².
Но по (3′) a² + d² + h² = 81, поэтому
85 – h² = 81 ⇒ h² = 4 ⇒ h = 2.
Следовательно, расстояние от точки K до плоскости прямоугольника ABCD равно 2.
AD^2=BC^2=32. В Δ AKD ∠ A=90*.Искомое расстояние
AK=sqrt(36-32) =2.