Задача 80591 Решите систему линейных алгебраических...
Условие
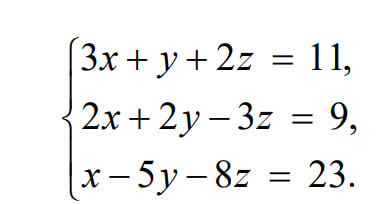
Решение
[m]A \cdot X = B[/m]
Здесь:
[m]A = \begin{pmatrix}
3 & 1 & 2 \\
2 & 2 & -3 \\
1 & -5 & -8 \\
\end{pmatrix};\ \ \ X = \begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix};\ \ \ B = \begin{pmatrix}
11 \\
9 \\
23 \\
\end{pmatrix}[/m]
Подставляем:
[m]\begin{pmatrix}
3 & 1 & 2 \\
2 & 2 & -3 \\
1 & -5 & -8 \\
\end{pmatrix}\ \cdot \begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}\ = \begin{pmatrix}
11 \\
9 \\
23 \\
\end{pmatrix}[/m]
Отсюда матрицу переменных можно найти умножением на обратную матрицу:
[m]X = A^{-1} \cdot B[/m]
Находим матрицу, обратную к матрице A.
1) Находим определитель |A|:
[m]|A| = \begin{vmatrix}
3 & 1 & 2 \\
2 & 2 & -3 \\
1 & -5 & -8 \\
\end{vmatrix} = [/m]
= 3*2(-8) + 2*2(-5) + 1*1(-3) - 2*2*1 - 3(-3)(-5) - 1*2(-8) = -48 - 20 - 3 - 4 - 45 + 16 = -104
[b]|A| = -104[/b]
2) Находим миноры и алгебраические дополнения матрицы A:
[m]M_{11} = \begin{vmatrix}
2 & -3 \\
-5 & -8 \\
\end{vmatrix} = 2(-8) - (-5)(-3) = -16 - 15 = -31;\ A_{11} = -31[/m]
[m]M_{12} = \begin{vmatrix}
2 & -3 \\
1 & -8 \\
\end{vmatrix} = 2(-8) - 1(-3) = -16 + 3 = -13;\ A_{12} = (-1)^{1+2} \cdot (-13) = 13[/m]
[m]M_{13} = \begin{vmatrix}
2 & 2 \\
1 & -5 \\
\end{vmatrix} = 2(-5) - 1 \cdot 2 = -10 - 2 = -12;\ A_{13} = (-1)^{1+3} \cdot (-12) = -12[/m]
[m]M_{21} = \begin{vmatrix}
1 & 2 \\
-5 & -8 \\
\end{vmatrix} = 1(-8) - (-5) \cdot 2 = -8 + 10 = 2;\ A_{21} = (-1)^{2+1} \cdot 2 = -2[/m]
[m]M_{22} = \begin{vmatrix}
3 & 2 \\
1 & -8 \\
\end{vmatrix} = 3(-8) - 1 \cdot 2 = -24 - 2 = -26;\ A_{22} = (-1)^{2+2} \cdot (-26) = -26[/m]
[m]M_{23} = \begin{vmatrix}
3 & 1 \\
1 & -5 \\
\end{vmatrix} = 3(-5) - 1 \cdot 1 = -15 - 1 = -16;\ A_{23} = (-1)^{2+3} \cdot (-16) = 16[/m]
[m]M_{31} = \begin{vmatrix}
1 & 2 \\
2 & -3 \\
\end{vmatrix} = 1(-3) - 2 \cdot 2 = -3 - 4 = -7;\ A_{31} = (-1)^{3+1} \cdot (-7) = -7[/m]
[m]M_{32} = \begin{vmatrix}
3 & 2 \\
2 & -3 \\
\end{vmatrix} = 3(-3) - 2 \cdot 2 = -9 - 4 = -13;\ A_{32} = (-1)^{3+2} \cdot (-13) = 13[/m]
[m]M_{33} = \begin{vmatrix}
3 & 1 \\
2 & 2 \\
\end{vmatrix} = 3 \cdot 2 - 2 \cdot 1 = 6 - 2 = 4;\ A_{33} = (-1)^{3+3} \cdot 4 = 4[/m]
3) Собираем матрицу алгебраических дополнений и транспонируем ее:
[m]A_{ij} = \begin{pmatrix}
A_{11} & A_{12} & A_{13} \\
A_{21} & A_{22} & A_{23} \\
A_{31} & A_{32} & A_{33} \\
\end{pmatrix} = \begin{pmatrix}
-31 & 13 & -12 \\
-2 & -26 & 16 \\
-7 & 13 & 4 \\
\end{pmatrix};\ \ \ A_{ij}^{T} = \begin{pmatrix}
-31 & -2 & -7 \\
13 & -26 & 13 \\
-12 & 16 & 4 \\
\end{pmatrix}[/m]
4) И, наконец, обратная матрица:
[m]A^{-1} = \frac{1}{|A|} \cdot A_{ij}^{T} = \begin{pmatrix}
31/104 & 2/104 & 7/104 \\
-13/104 & 26/104 & -13/104 \\
12/104 & -16/104 & -4/104 \\
\end{pmatrix}[/m]
Находим матрицу переменных умножением:
[m]X = A^{-1} \cdot B = \begin{pmatrix}
31/104 & 2/104 & 7/104 \\
-13/104 & 26/104 & -13/104 \\
12/104 & -16/104 & -4/104 \\
\end{pmatrix} \cdot \begin{pmatrix}
11 \\
9 \\
23 \\
\end{pmatrix} =[/m]
[m]\begin{pmatrix}
31/104 \cdot 11 + 2/104 \cdot 9 + 7/104 \cdot 23 \\
-13/104 \cdot 11 + 26/104 \cdot 9 - 13/104 \cdot 23 \\
12/104 \cdot 11 - 16/104 \cdot 9 - 4/104 \cdot 23 \\
\end{pmatrix} =[/m]
[m]= \begin{pmatrix}
(341 + 18 + 161)/104 \\
(-143 + 234 - 299)/104 \\
(132 - 144 - 92)/104 \\
\end{pmatrix} = \begin{pmatrix}
520/104 \\
-208/104 \\
-104/104 \\
\end{pmatrix} = \begin{pmatrix}
5 \\
-2 \\
-1 \\
\end{pmatrix}[/m]
Ответ: [b]x = 5; y = -2; z = -1[/b]