Задача 80582 ...
Условие
Решение
[m]cos(2x+\frac{π}{3}) ≤ \frac{1}{2}[/m]
Замена переменной
[m]2x+\frac{π}{3}=t[/m]
Решаем неравенство
[m]cos t≤ \frac{1}{2}[/m]
Решаем с помощью единичной окружности
[m]\frac{π}{3}+2πn ≤ t ≤-\frac{π}{3}+2π+2πn [/m],n ∈ Z
[m]\frac{π}{3}+2πn ≤ t ≤\frac{5π}{3}+2πn [/m],n ∈ Z
Обратный переход
[m]\frac{π}{3}+2πn ≤ 2x+\frac{π}{3} ≤\frac{5π}{3}+2πn [/m],n ∈ Z
Вычитаем от трех частей неравенства [m]\frac{π}{3} [/m], n ∈ Z
получаем:
[m]\frac{π}{3}-\frac{π}{3} +2πn ≤ 2x+\frac{π}{3}-\frac{π}{3} ≤\frac{5π}{3}-\frac{π}{3} +2πn [/m], n ∈ Z
[m]2πn ≤ 2x ≤\frac{4π}{3} +2πn [/m], n ∈ Z
Делим на 2
[m]πn ≤ x ≤\frac{4π}{6} +πn [/m], n ∈ Z
[b]Ответ.[/b]
[red][m]πn ≤ x ≤\frac{2π}{3} +πn [/m][/red], [red]n ∈ Z[/red]
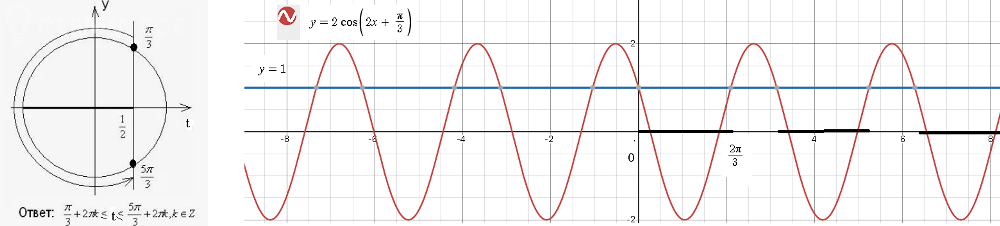
[i]Графическое решение.[/i]
Строим график функции
y=2cos(2x+(π/3))
Строим график прямой
y=1
Cм. рис справа
Ответ тот же