Задача 80581 21,6(1,2) 21.7(2)...
Условие

Решение
1) 2cos(2x + π/3) ≤ 1
cos(2x + π/3) ≤ 1/2
Замена 2x + π/3 = t
cos t ≤ 1/2
Записываем двойное неравенство с периодом 2k, k ∈ Z:
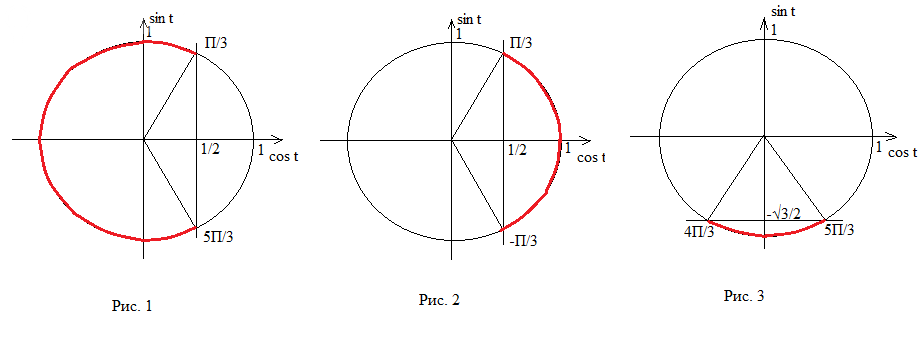
π/3 + 2π·k ≤ t ≤ 5π/3 + 2π·k, k ∈ Z
Решение показано на рис. 1 красным цветом.
Я специально сделал замену, чтобы нагляднее показать решение,
хотя это решение для всей скобки, а не для x. Переходим к x:
π/3 + 2π·k ≤ 2x + π/3 ≤ 5π/3 + 2π·k, k ∈ Z
Вычитаем π/3 из всех трёх выражений:
0 + 2π·k ≤ 2x ≤ 4π/3 + 2π·k, k ∈ Z
2π·k ≤ 2x ≤ 4π/3 + 2π·k, k ∈ Z
Делим на 2 все три выражения:
π·k ≤ x ≤ 2π/3 + π·k, k ∈ Z
[b]x ∈ [π·k; 2π/3 + π·k], k ∈ Z[/b]
2) 2cos(4x – π/6) > 1
cos(4x – π/6) > 1/2
Замена 4x – π/6 = t
cos t > 1/2
–π/3 + 2π·k < t < π/3 + 2π·k, k ∈ Z
Решение показано на рис. 2 красным цветом.
–π/3 + 2π·k < 4x – π/6 < π/3 + 2π·k, k ∈ Z
–2π/6 + 2π·k < 4x – π/6 < 2π/6 + 2π·k, k ∈ Z
–π/6 + 2π·k < 4x < 3π/6 + 2π·k, k ∈ Z
–π/6 + 2π·k < 4x < π/2 + 2π·k, k ∈ Z
–π/24 + π/2·k < x < π/8 + π/2·k, k ∈ Z
[b]x ∈ (–π/24 + π/2·k; π/8 + π/2·k), k ∈ Z[/b]
21.7. 2) sin x*cos π/4 - cos x*sin π/4 < -sqrt(3)/2
По формуле синуса разности:
sin (x - π/4) < -sqrt(3)/2
Замена x - π/4 = t
sin t < -sqrt(3)/2
4π/3 + 2π*k < t < 5π/3 + 2π*k, k ∈ Z
Решение показано на рис. 3 красным цветом.
4π/3 + 2π*k < x - π/4 < 5π/3 + 2π*k, k ∈ Z
4π/3 + π/4 + 2π*k < x < 5π/3 + π/4 + 2π*k, k ∈ Z
16π/12 + 3π/12 + 2π*k < x < 20π/12 + 3π/12 + 2π*k, k ∈ Z
19π/12 + 2π*k < x < 23π/12 + 2π*k, k ∈ Z
[b]x ∈ (19π/12 + 2π*k; 23π/12 + 2π*k), k ∈ Z[/b]