Задача 80578 ...

692561dfa0211e4a1fadc0f5

11/25/2025 7:59:45 AM

Из точки А на плоскость α проведены две наклонные АВ=АС=6см. Угол между ними равен 60 ° а между их проекциями 90 °. Найти расстояние от точки А до плоскости α

626fab9a354ab65fb2f43abb

11/25/2025 9:28:51 AM

★

Смотрите рисунок.
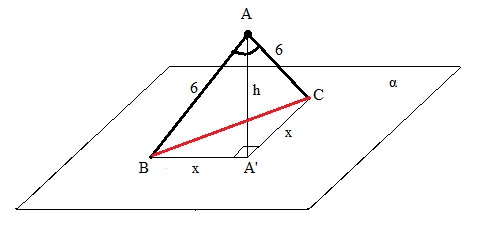
|AB| = |AC| = 6 см, ∠ BAC = 60°, ∠ BA'C = 90°
Обозначим проекции A'B = A'C = x см,
высота точки А над плоскостью α: AA' = h = ?.
Проведем дополнительно отрезок BC, он показан красным.
Треугольник ABC - равнобедренный с ∠ BAC = 60°.
Два остальных угла равны друг другу и равны:
∠ ABC = ∠ ACB = (180° - 60°)/2 = 120°/2 = 60°
Значит, ABC - равносторонний треугольник.
|BC| = |AB| = |AC| = 6 см.
Треугольник A'BC - равнобедренный и прямоугольный, поэтому:
x = |A'B| = |A'C| = |BC|/sqrt(2) = 6/sqrt(2) = 3sqrt(2) см
И, наконец, треугольник AA'B - прямоугольный.
По теореме Пифагора:
h^2 = |AA'|^2 = |AB|^2 - |A'B|^2 = 6^2 - (3sqrt(2))^2 = 36 - 18 = 18
h = sqrt(18) = 3sqrt(2) см
Оказывается, треугольники AA'B и AA'C - тоже прямоугольные и равнобедренные, причем такие же, как A'BC.

Ответ: 3sqrt(2) см