Задача 80576 ...
Условие

Решение
1) Найти область определения.
z = ln(4 - x^2 - y^2)
Выражение под логарифмом больше 0
4 - x^2 - y^2 > 0
x^2 + y^2 < 4
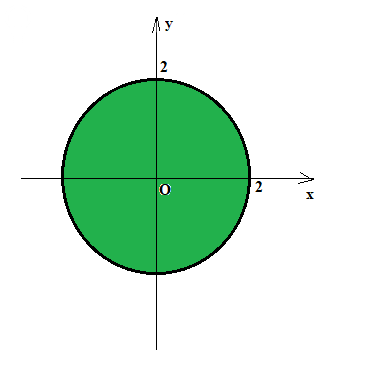
Это внутренняя область круга радиусом R = sqrt(4) = 2
Он показан на рисунке зеленым цветом.
Задача 2.
1) Найти частные производные и полный дифференциал.
z = arcsin sqrt(xy)
[m]\large \frac{dz}{dx} = \frac{1}{\sqrt{1 - xy}} \cdot \frac{1}{2\sqrt{xy}} \cdot y = \frac{1}{\sqrt{1 - xy}} \cdot \frac{\sqrt{y}}{2\sqrt{x}}[/m]
[m]\large \frac{dz}{dy} = \frac{1}{\sqrt{1 - xy}} \cdot \frac{1}{2\sqrt{xy}} \cdot x = \frac{1}{\sqrt{1 - xy}} \cdot \frac{\sqrt{x}}{2\sqrt{y}}[/m]
Полный дифференциал:
[m]\large dz = \frac{1}{\sqrt{1 - xy}} \cdot \frac{\sqrt{y}}{2\sqrt{x}} dx + \frac{1}{\sqrt{1 - xy}} \cdot \frac{\sqrt{x}}{2\sqrt{y}} dy[/m]